Question

A transverse harmonic wave on a string is described by y(x,t) = 3.0sin(36t+0.018x+$\pi /4$), where x and y are in cm and t in s. The positive direction of x is from left to right.
For the wave described in the above exercise, plot the displacement(y) versus (t) graph for x=0, 2 and 4cm. What are the shapes of these graphs? In which aspect does the oscillatory motion in a travelling wave differ from one point to another: amplitude, frequency or phase?

Answer 1

The particular transfer of the energy from one point to another by the perpendicular vibration in the direction of the wave propagation is known as the transverse waves.
To solve this type of question use the following formula.
$v = \dfrac{\omega }{k}$ ; Where $\omega$ is frequency, k is propagation constant and v is velocity.
$k = \dfrac{{2\pi }}{\lambda }$; Where $\lambda$ is wavelength.
$y(x,t) = A\sin (\omega t + kx + \phi )$ ; This the general form of wave. Where, $A$ is amplitude, $\omega$ is frequency, k is wave vector and $\phi$ is phase angle.

Complete step-by-step answer:
Following information is given in question: $y(x,t) = 3\sin \left( {36t + 0.018x + \dfrac{\pi }{4}} \right)$
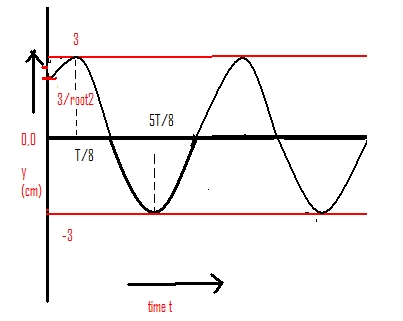
Now let use draw the graph when x=0. So, the expression becomes, $y(0,t) = 3\sin \left( {36t + \dfrac{\pi }{4}} \right)$.
Following is the graph between displacement and time t.
When, t=0, y=$\dfrac{3}{{\sqrt 2 }}$ so graph will start from $\left( {0,\dfrac{3}{{\sqrt 2 }}} \right)$

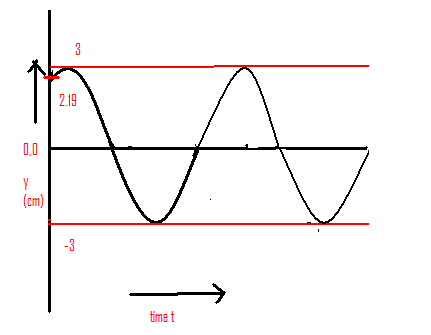
This is the graph when x=2 and displacement of wave becomes, $y(x,t) = 3\sin (36t + 0.036 + \dfrac{\pi }{4})$

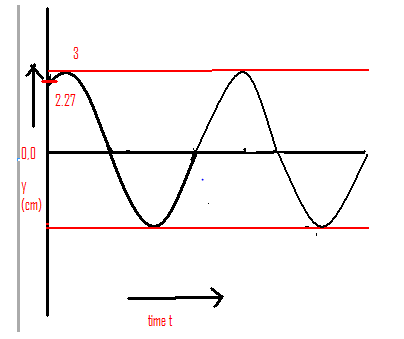
This is the graph when, x=4 and displacement become, $y(x,t) = 3\sin (36t + 0.072 + \dfrac{\pi }{4})$

Let us compare this formula with the general form of wave equation $y(x,t) = A\sin (\omega t + kx + \phi )$
We get the following.
A=3cm, $\omega$=36, k=0.018, $\phi$=$\dfrac{\pi }{4}$.
So from the above collected data we can write.
Amplitude of the wave is 3 cm, phase angle is$\dfrac{\pi }{4}$ and frequency is 36.
Now, let us find the linear frequency using $f = \dfrac{{2\pi }}{\omega }$
Let us substitute the value and solve it.
$f = \dfrac{{2\pi }}{{36}}$
$= 0.1744{s^{ - 1}}$
Similarly, we can find the speed of wave using the formula $v = \dfrac{\omega }{k}$
Let us substitute the value and solve it.
$v = \dfrac{{36}}{{0.018}}$
$= 2000cm/s$
Now, let us find the wavelength using formula $k = \dfrac{{2\pi }}{\lambda }$
Let us substitute the values.
$\lambda = \dfrac{{2\pi }}{{0.018}}$
$= 348.89cm$

Note: All the graphs have the same frequency and amplitude but the initial phase is different for all. The graphs are sinusoidal in shape.