Question

A transparent thin film of uniform thickness and refractive index ${{n}_{1}}=1.4$ is coated on the convex spherical surface of radius R at one end of a long solid glass cylinder of refractive index ${{n}_{2}}=1.5$, as shown in the figure. Rays of light parallel to the axis of the cylinder traversing through the film from air to glass get focused at distance ${{f}_{1}}$ from the film, while rays of light traversing from glass to air get focused at distance ${{f}_{2}}$ from the film. Then
$\begin{aligned} & \text{A}.\text{ }\left| {{f}_{1}} \right|=3R \\\ & \text{B}\text{. }\left| {{f}_{1}} \right|=2.8R \\\ & \text{C}\text{. }\left| {{f}_{2}} \right|=2R \\\ & D.\text{ }\left| {{f}_{2}} \right|=1.4R \\\ \end{aligned}$

Answer 1

This kind of question can be solved by taking two cases separately. Take one case from air to glass and second from glass to air. Use formula for refraction at a single curved surface. This formula gives relation among image distance, object distance, Radius of curvature, medium where image has formed and medium where object has placed. Use sign convention to specify position of image and object.

Complete step-by-step answer :
In this question we need to calculate value of ${{f}_{1}}$ and ${{f}_{2}}$
Air to glass:

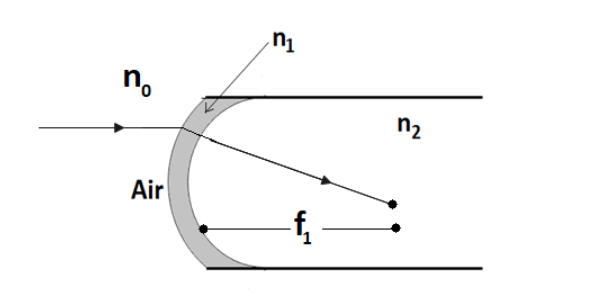
Consider a case where ray AB incident on outer portion of convex lens, entering from air ${{n}_{0}}=1$ medium to ${{n}_{1}}=1.4$ and then from ${{n}_{1}}=1.4$ to ${{n}_{2}}=1.5$.
Ray AB is coming from infinity, therefore object distance is infinity in medium ${{n}_{0}}=1$
In this case, image has formed at ${{f}_{1}}$ in medium i.e. at ${{n}_{2}}=1.5$
Formula for refraction at single curved surface is given by,
$\dfrac{{{\mu }_{2}}}{v}+\dfrac{{{\mu }_{1}}}{u}=\dfrac{({{\mu }_{2}}-{{\mu }_{1}})}{R}$
Where,
u= object distance
v= image distance
${\mu }_{1}$= refractive index of medium where object has placed
${\mu }_{2}$= refractive index of medium where image has formed
R= radius of curvature

Since the ray AB incident from the left side of the convex lens to the right side. Therefore the left side must be negative and the right side must be positive according to sign convention. Therefore sign of object must be negative and sign of image & $R$ must be positive, according to sign convention.
$\text{Therefore, }u=-\infty ,v=+{{f}_{1,}} R=+R$.
Put value in above formula we get,
$\begin{aligned} & \dfrac{1.5}{{{f}_{1}}}-\dfrac{1}{\infty }=\dfrac{(1.5-1)}{R} \\\ & \dfrac{1.5}{{{f}_{1}}}=\dfrac{0.5}{R} \\\ & {{f}_{1}}=3R \\\ \end{aligned}$
Glass to air:

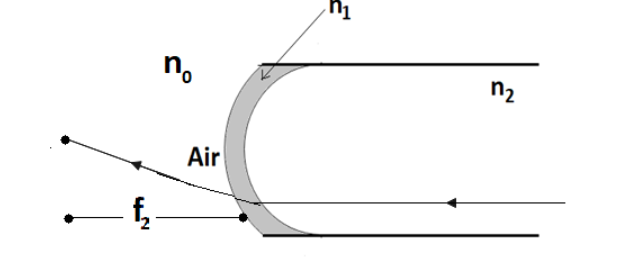
Now consider a case ray CD incident on inner portion of convex lens, entering from glass ${{n}_{2}}=1.5$ medium to ${{n}_{1}}=1.4$ and then from ${{n}_{1}}=1.4$ to ${{n}_{0}}=1$.
Ray CD is coming from infinity, therefore object distance is infinity in medium,${{n}_{2}}=1.5$
In this case, the image has formed at ${{f}_{2}}$in medium${{n}_{0}}=1$.
Since the ray CD incident from the right side of the convex lens to the left side. Therefore the right side must be negative and the left side must be positive, according to sign convention. Therefore sign of object & $R$ must be negative and sign of image must be positive, according to sign convention.
$\text{Therefore, }u=-\infty ,R=-R,v=+{{f}_{2}}$
Put value in above formula we get,
$\begin{aligned} & \dfrac{1}{{{f}_{2}}}-\dfrac{1.5}{\infty }=\dfrac{(1-1.5)}{-R} \\\ & \dfrac{1}{{{f}_{2}}}=\dfrac{0.5}{R} \\\ & {{f}_{2}}=2R \\\ \end{aligned}$
Hence the correct options are A and C

Note : If ray incident from left side of convex lens to right side then left side must be negative and right side must be positive according to sign convention. If the ray incident from right side of convex lens to left then right side must be negative and left side must be positive, according to sign convention. $\dfrac{{{\mu }_{2}}}{v}+\dfrac{{{\mu }_{1}}}{u}=\dfrac{({{\mu }_{2}}-{{\mu }_{1}})}{R}$ relation is applicable for real as well as virtual image and for ant pair of refracting media. While using this expression, the quantities $u,v,R$ are to be used with their appropriate sign.