Question

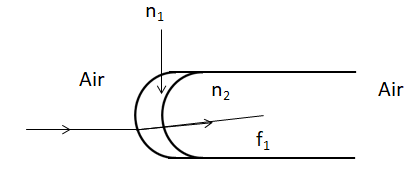
A transparent thin film of refractive index ${{n}_{1}}=1.4$ is coated on the convex spherical surface of radius R at one end of a long solid glass cylinder of refractive index ${{n}_{2}}=1.5$, as shown in the figure. Rays of light parallel to the axis of cylinder traversing through the film from air to glass get focused at distance ${{f}_{1}}$ from the cylinder, while rays of light traversing from glass to air get focused at distance ${{f}_{2}}$ from the thin film. Then:

$A.\quad \left| {{f}_{1}} \right|=3R$
$B.\quad \left| {{f}_{1}} \right|=2.8R$
$C.\quad \left| {{f}_{2}} \right|=2R$
$D.\quad \left| {{f}_{2}} \right|=1.4R$

Answer 1

Hint :
We need to remember that for the case of spherical surfaces, there wouldn’t be any effect of the thin film of refractive index ${{n}_{1}}=1.4$ on the system of air and the spherical surface. To solve this problem we will use a special conditioned formula of the lens makers formula, which is: $-\dfrac{{{\mu }_{1}}}{u}+\dfrac{{{\mu }_{2}}}{v}=\dfrac{{{\mu }_{2}}-{{\mu }_{1}}}{R}$, where the refractive indices are given by $\mu$.

Step by step solution:
In this problem, we need to remember that whenever a thin film if applied over a spherical surface being surrounded by the common medium such as air, there wouldn’t be any effect of the thin film’s refraction.
Let’s consider the case, when rays parallel to the axis of the cylinder, traverse from air through the thin film to the spherical surface glass cylinder. As per the problem, these parallel rays focus at the distance ${{f}_{1}}$ from the cylinder’s spherical surface. We also know that the spherical surface’s radius of curvature is R.

We will now use the special condition of the formula of the lens makers formula, which is: $-\dfrac{{{\mu }_{1}}}{u}+\dfrac{{{\mu }_{2}}}{v}=\dfrac{{{\mu }_{2}}-{{\mu }_{1}}}{R}$. In this case, since the rays are parallel, hence the object distance is infinity.
Hence, $u=\infty$. Further, ${{\mu }_{1}}=1$in this case, since the rays emerge from air, having refractive index of 1 and ${{\mu }_{2}}={{n}_{2}}=1.5$, since that is the refractive index of the glass cylinder. Lastly, the image distance is: $v={{f}_{1}}$. Therefore: $-\dfrac{{{\mu }_{1}}}{u}+\dfrac{{{\mu }_{2}}}{v}=\dfrac{{{\mu }_{2}}-{{\mu }_{1}}}{R}\Rightarrow -\dfrac{1}{\infty }+\dfrac{1.5}{{{f}_{1}}}=\dfrac{1.5-1}{R}\Rightarrow \dfrac{1.5}{{{f}_{1}}}=\dfrac{0.5}{R}\Rightarrow {{f}_{1}}=3R$.
Now, let’s consider the case, when rays parallel to the axis of the cylinder, traverse from the spherical surface glass cylinder through the thin film to air. As per the problem, these parallel rays focus at the distance ${{f}_{2}}$ from the thin film.

Again using the formula: $-\dfrac{{{\mu }_{1}}}{u}+\dfrac{{{\mu }_{2}}}{v}=\dfrac{{{\mu }_{2}}-{{\mu }_{1}}}{R}$. In this case again, the rays are parallel, hence the object distance is infinity. Hence, $u=\infty$. Further, ${{\mu }_{2}}=1$ in this case, since the refractive index of air is 1 and ${{\mu }_{1}}={{n}_{2}}=1.5$, since that is the refractive index of the glass cylinder. Lastly, the image distance is: $v={{f}_{2}}$. Therefore: $-\dfrac{{{\mu }_{1}}}{u}+\dfrac{{{\mu }_{2}}}{v}=\dfrac{{{\mu }_{2}}-{{\mu }_{1}}}{R}\Rightarrow -\dfrac{1.5}{\infty }+\dfrac{1}{{{f}_{2}}}=\dfrac{1-1.5}{-R}\Rightarrow \dfrac{1}{{{f}_{2}}}=\dfrac{-0.5}{-R}\Rightarrow {{f}_{2}}=2R$.
Therefore, the Options (A) and (C) are the solutions.

Note :
For the second case, when the rays parallel to the axis of the cylinder, traverse from the spherical surface glass cylinder through the thin film to air, the value of the radius of curvature of the spherical surface is (-R). This happened because, to find the value of the radius of the curvature of the spherical surface, we travel against the direction of the ray. Therefore, the value of the radius of curvature is negative in this case.