Solveeit Logo
Login

Question

Question: A transparent solid cylindrical rod has a refractive index of \(\dfrac{2}{{\sqrt 3 }}\). It is surro...

A transparent solid cylindrical rod has a refractive index of 23\dfrac{2}{{\sqrt 3 }}. It is surrounded by air. The light ray is incident at the mid-point of one end of the rod as shown in the figure. The incident angle θ\theta for which the light ray grazes along the wall of the rod is-

(A) sin⁡−1(12){\sin ^{ - 1}}\left( {\dfrac{1}{2}} \right)
(B) sin⁡−1(32){\sin ^{ - 1}}\left( {\dfrac{{\sqrt 3 }}{2}} \right)
(C) sin⁡−1(23){\sin ^{ - 1}}\left( {\dfrac{2}{{\sqrt 3 }}} \right)
(D) sin⁡−1(13){\sin ^{ - 1}}\left( {\dfrac{1}{{\sqrt 3 }}} \right)

Explanation

Solution

The angle at which the ray is incident on the inside of the rod is the critical angle. As the sine of the critical angle is the inverse of the refractive index, we can get the critical angle. Now from geometry, we get the angle of refraction. So from Snell’s law, we can get the angle θ\theta .
Formula Used: In this solution we will be using the following formula,
⇒sin⁡isin⁡r=n2n1\Rightarrow \dfrac{{\sin i}}{{\sin r}} = \dfrac{{{n_2}}}{{{n_1}}}
where ii is the angle of incidence, rr is the angle of refraction and n1{n_1} is the refractive index of the material the incident ray is present and n2{n_2} is the refractive index of the material the refracted ray is present.

Complete step by step solution:
To find the answer we first need to redraw the diagram as,

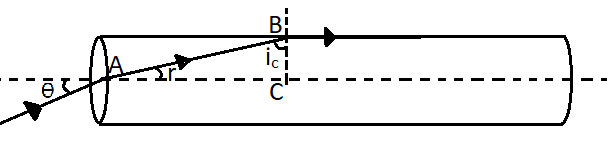
We can see that the ray inside the cylindrical rod strikes at point B at an angle such that the angle of refraction is 90∘90^\circ . So we can apply Snell's law at point B. Here the first medium is the glass having the refractive index of 23\dfrac{2}{{\sqrt 3 }} and the second medium is air having a refractive index of 1. So, n1=23{n_1} = \dfrac{2}{{\sqrt 3 }} and n2=1{n_2} = 1. Therefore, from Snell’s law,
⇒sin⁡icsin⁡r=n2n1\Rightarrow \dfrac{{\sin {i_c}}}{{\sin r}} = \dfrac{{{n_2}}}{{{n_1}}}
So substituting the values we get,
⇒sin⁡icsin⁡90=123\Rightarrow \dfrac{{\sin {i_c}}}{{\sin 90}} = \dfrac{1}{{\dfrac{2}{{\sqrt 3 }}}}
So we get, the critical angle as,
⇒ic=sin⁡−1(32)\Rightarrow {i_c} = {\sin ^{ - 1}}\left( {\dfrac{{\sqrt 3 }}{2}} \right)
Since, sin⁡60=32\sin 60 = \dfrac{{\sqrt 3 }}{2}
So we get, ic=60∘{i_c} = 60^\circ
Now from the triangle ABC, we can see that the sum of the critical angle and the angle of refraction is 90∘90^\circ .
Therefore, r+ic=90∘r + {i_c} = 90^\circ
Now substituting the values we get,
⇒r=90∘−60∘=30∘\Rightarrow r = 90^\circ - 60^\circ = 30^\circ
Now again we can apply the Snell’s law at the point A. Here, the first medium has a refractive index of n1=1{n_1} = 1 and the second medium has a refractive index of, n2=23{n_2} = \dfrac{2}{{\sqrt 3 }}
So using the Snell’s law we get,
⇒sin⁡θsin⁡30=23\Rightarrow \dfrac{{\sin \theta }}{{\sin 30}} = \dfrac{2}{{\sqrt 3 }}
So we get, sin⁡θ=sin⁡30×23\sin \theta = \sin 30 \times \dfrac{2}{{\sqrt 3 }}
Since the value of sin⁡30=12\sin 30 = \dfrac{1}{2}
Substituting we get,
⇒sin⁡θ=12×23\Rightarrow \sin \theta = \dfrac{1}{2} \times \dfrac{2}{{\sqrt 3 }}
Therefore, sin⁡θ=13\sin \theta = \dfrac{1}{{\sqrt 3 }}
So we get the angle as,
⇒θ=sin⁡−113\Rightarrow \theta = {\sin ^{ - 1}}\dfrac{1}{{\sqrt 3 }}
So the correct answer is option (D).

Note:
The Snell’s law is a formula that is used to describe the angle of incidence to the angle of refraction. The ratio of the sine of the two angles can also be written as the ratio of the phase velocity of the wave in the two media.