Question

A transparent cube contains a small air bubble. Its apparent is $2cm$ when seen through one face and $5cm$ when seen through another face. If the refractive index of the material of the cube is 1.5, the real length of the edge of the cube must be:
A. $7cm$
B. $7.5cm$
C. $10.5cm$
D. $\dfrac{14}{3}cm$

Answer 1

Hint: This problem can be solved by drawing a proper diagram and applying the formula for refraction at a spherical interface and extending it to the plane form by considering the radius of the sphere to be infinity (for a plane). The distance of the bubble from both edges can be found out as it will be the object distance in each case and the total length of the edge can be calculated by summing them up.

Formula used:
For refraction through at a spherical interface of radius $R$ with a medium of refractive index ${{n}_{1}}$ on the object side and that of ${{n}_{2}}$ on the other side of the interface, the mathematical formula relating the object distance $u$ and the image distance $v$ is given by,
$\dfrac{{{n}_{2}}}{v}-\dfrac{{{n}_{1}}}{u}=\dfrac{{{n}_{2}}-{{n}_{1}}}{R}$

Complete step-by-step answer:
First let us draw a diagram to understand the problem better.

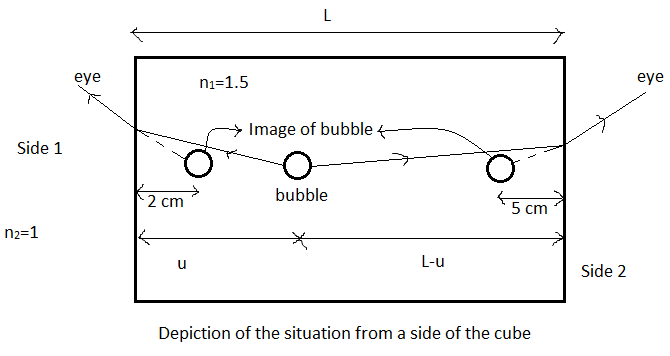
We are given that there is a bubble inside a cube and when seen from one side its apparent image is at $2cm$ from the edge and when seen from the other side, it is at $5cm$ from the edge.
As marked in the figure, let the bubble be at a distance $u$ from the edge of side 1. Let the total length of the edge be $L$. Therefore, obviously from side 2, the bubble will be at a distance of $L-u$ from the edge.
Now, we are given the apparent distances from the two edges, that is they are the image distances of the bubble when viewed from each edge respectively.
The refractive index of the cube is given to be ${{n}_{1}}=1.5$.
Now, we can solve this problem by applying the formula relating the object distances and image distances during refraction at a spherical interface having media of different refractive indices on either side. The plane of the cube can be considered as a spherical interface with radius as infinity.
For refraction through at a spherical interface of radius $R$ with a medium of refractive index ${{n}_{1}}$ on the object side and that of ${{n}_{2}}$ on the other side of the interface, the mathematical formula relating the object distance $u$ and the image distance $v$ is given by,
$\dfrac{{{n}_{2}}}{v}-\dfrac{{{n}_{1}}}{u}=\dfrac{{{n}_{2}}-{{n}_{1}}}{R}$ --(1)
For refraction on side 1 of the interface, ${{n}_{2}}=1$ -(since it is air) $v=2cm$ $u=u$ ${{n}_{1}}=1.5$ $R=\infty$ (as explained above for plane surfaces)
Therefore, plugging in these values in equation (1), we get,
$\dfrac{1}{2}-\dfrac{1.5}{u}=\dfrac{\left| 1-1.5 \right|}{\infty }$ $\therefore \dfrac{1}{2}-\dfrac{1.5}{u}=0$ --$\left( \because \dfrac{1}{\infty }=0 \right)$ $\therefore \dfrac{1}{2}=\dfrac{1.5}{u}$ $\therefore u=1.5\times 2=3cm$ --(2)
Similarly, for refraction on side 2 of the interface,
${{n}_{2}}=1$ -(since it is air) $v=5cm$ $u=L-u$ ${{n}_{1}}=1.5$ $R=\infty$ (as explained above for plane surfaces)
Therefore, plugging in these values in equation (1), we get,
$\dfrac{1}{5}-\dfrac{1.5}{L-u}=\dfrac{\left| 1-1.5 \right|}{\infty }$ $\therefore \dfrac{1}{5}-\dfrac{1.5}{L-u}=0$ --$\left( \because \dfrac{1}{\infty }=0 \right)$ $\therefore \dfrac{1}{5}=\dfrac{1.5}{L-u}$ $\therefore L-u=1.5\times 5=7.5cm$ --(3)
Now, adding (2) and (3), we get,
$u+L-u=3+7.5$ $\therefore L=10.5cm$
Hence, the length of the edge is$10.5cm$.
Hence, the correct option is C) $10.5cm$.

Note: The best way to solve problems of optics is to draw diagrams. This helps in visualizing the problem clearly, since the topic is not as intuitive as something like mechanics.
For example, this question has a lot of information given in a lot of words. The student may very easily get confused and not be able to proceed further with this question, let alone solve it without a diagram. By drawing a diagram at first by analyzing all the information given and incorporating them into the diagram, we are essentially converting the question into a diagram. This makes it a lot easier to solve the problem as now we can visualize what is happening in the problem and what all we are required to find to arrive at our answer.