Question
Question: A transmitting antenna of height \(h\) and the receiving antenna of height \(\dfrac{3}{4}h\) are sep...
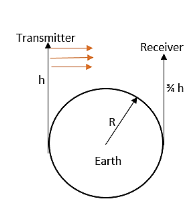
A transmitting antenna of height h and the receiving antenna of height 43h are separated by a distance of d for satisfactory communication in line-of-sight mode. Then, the value of h is
[Given, the radius of the earth is R].
A.2Rd2(22−6)2B.4Rd2(22−6)2C.Rd2(22−6)2D.8Rd2(22−6)2
Solution
The height of antenna can be calculated using the equation,
dm=2RhT+2RhR
Where dm be the maximum distance of line of sight between the antenna and the transmitting antenna. Then after solving and rearranging we will get the value of dm in terms of h. The denominator of the term is factorized after this and then squares the both sides of the equation. This will lead you to the answer.
Complete answer:
first of all let us look at what all are given in the question.
The height of the transmitting antenna has been given as the equation,
hT=h
And also the height of the receiving antenna is given by the equation,
hR=43h
As we know the radius of the earth is R.
The maximum line of sight distance between these two antenna is given by the equation,
dm=2RhT+2RhR
In the question, it is mentioned that the value of dmis,
dm=d
Substituting all these values in it will give,
