Question

A transformer steps up an AC supply from 220V to 2200V. if these secondary coil of the transformer has 2000 turns, the number of turns in its primary coil will be:
A) $200$
B) $100$
C) $50$
D) $20$

Answer 1

The power in primary coil is equal to the power in secondary coil and the concept of power in coil is used to give the relationship between the number of turns and voltage of the coil. The number of turns in a coil is directly proportional to the voltage of the coil.

Complete step by step solution:

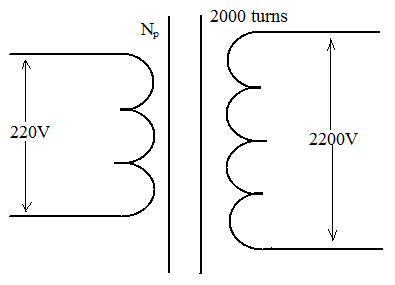
The transformer is of two types: step up transformer and step down transformer.
The step up transformer is used to increase the voltage from primary to secondary voltage. And also, the number of turns in primary winding is less than the number of turns in secondary winding.
The step down transformer is used to decrease the voltage from primary to secondary voltage. And also, the number of turns in primary winding is more than the number of turns in secondary winding.
We can calculate the number of turns in the primary coil with the help of the ratio of voltages.
$\Rightarrow \dfrac{{{N_s}}}{{{N_p}}} = \dfrac{{{V_s}}}{{{V_p}}}$
Here, the number of turns in primary coil is ${N_p}$, the number of turns in secondary coil is ${N_s}$, the voltage of primary coil is ${V_p}$ and the voltage of secondary coil is ${V_s}$.
We will now substitute the known values in the relation between the voltages and the number of turns.
$\Rightarrow \dfrac{{2000}}{{{N_p}}} = \dfrac{{2200}}{{220}}\\\ \Rightarrow \dfrac{{2000}}{{{N_p}}} = 10\\\ \Rightarrow {N_p} = \dfrac{{2000}}{{10}}\\\ \Rightarrow 200$
Thus, the number of turns in the primary coil is calculated to be $200$.

Thus from the given options, only option A is correct.

Note: The output voltage of a transformer changes with the change in load even if the output voltage of the transformer remains constant. The transformer equation is also used to solve the given question.