Question
Question: A train of mass M is moving on a circular track of radius \(R\) with a constant speed \(v\). The len...
A train of mass M is moving on a circular track of radius R with a constant speed v. The length of the train is half of the perimeter of the track. Find the linear momentum of the train.
A) Zero
B) π2Mv
C) MvR
D) Mv
Solution
Here the length of the train is given to be half of the perimeter of the circular track. The velocity of the train is said to be constant. But only its magnitude remains constant, at different points on the track, the direction of the velocity varies. The linear momentum of the train can thus be obtained by integrating the momentum of a small element on the circular track.
Formula used:
The linear momentum of a body is given by,
p=mv, where m is the mass of the body and v is the velocity of the body.
The linear density of an object is given by,
λ=lm, where m is the mass of the object and l is the length of the object.
Complete step by step answer:
Step 1: Sketch a figure depicting the motion of the train along the circular track and list the parameters given in the question.
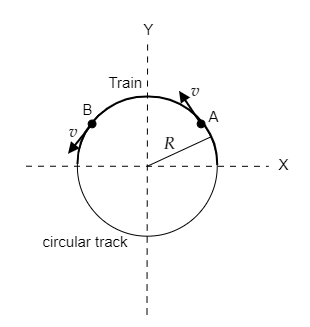
The above figure depicts the train along the circular track. As shown in the figure, the train is symmetrical about the Y-axis. A and B represent the two points which are symmetrical about the Y-axis and which correspond to two points in the motion of the train. The velocity v at these two points (or any point along the circle) will have a vertical component and a horizontal component.
The mass of the train is given to be M .
The radius of the circular track is given to be R and its perimeter will be 2πR .
Let l be the length of the train. As mentioned in the question the length of the train can be expressed as l=22πR=πR .
The mass per unit length or the linear density of the train will be λ=lM=πRM .
Step 2: Consider a small element of the train to obtain an expression for its linear momentum.
We now consider a small element making an angle θ with the X-axis. This element subtends an angle dθ. This is shown in the figure below.
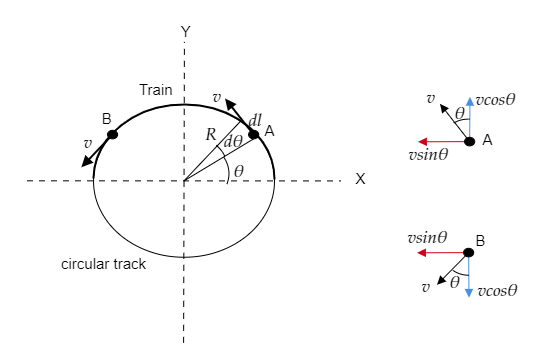
The length of the small element will be dl=Rdθ .
Then the mass of the small element can be expressed as dm=λdl -------- (1)
Substituting for λ=πRM and dl=Rdθ in equation (1) we get,
⇒dm=πRM×Rdθ=πMdθ
Thus the mass of the small element is dm=πMdθ .
From the above figure, we see that the vertical component of the velocity vcosθ at A and B is directed along the positive Y direction and negative Y direction respectively and so they will cancel out each other. Thus only the horizontal component vsinθ prevails.
Now we can express the linear momentum of the small element as dp=dm(vsinθ) ------- (2)
Substituting dm=πMdθ in equation (2) we get,
⇒dp=πM(vsinθ)dθ -------- (3)
Equation (3) expresses the linear momentum of the small element.
So integrating equation (3) will provide us with the total linear momentum of the train.
Step 3: Integrate equation (3) to obtain the total linear momentum.
The total linear momentum of the train is given by, P=0∫πdpx=0∫ππM(vsinθ)dθ --------(A)
Integrating the above expression we get,
⇒P=πMv0∫πsinθdθ=π−Mv[cosθ]0π ------- (4)
Applying the limits we get,
⇒P=π−Mv[−1−(+1)]=π2Mv ------ (5)
Thus the linear momentum of the train is obtained as P=π2Mv
Hence the correct option is B.
Note:
Here the start of the train is taken to be from X-axis and so for the length of the train, the angle θ varies from 0∘ to 180∘ and we have the lower limit of the integral given by equation (A) as zero and its upper limit as π. The integral of sinθ is −cosθ, this is substituted in equation (4). We have cosπ=−1 and cos0=+1, these values are substituted in equation (5). The direction of the linear momentum will be along the horizontal component of the velocity.
