Question

A train of mass M is moving on a circular track of radius R with a constant speed v. The length of the train is half of the perimeter of the track. The linear momentum of the train will be
A) Zero
B) $\dfrac{2Mv}{\pi }$
C) $MvR$
D) $Mv$

Answer 1

We will be using the integral method to find the linear momentum as the velocity of the train will change even if the speed remains constant as velocity is direction dependent meaning the velocity will change with the change in direction. The formula of the linear momentum with component is given as:
$P=\int{dm{{v}_{x}}}$
where $dm$ is the mass per unit length and length is taken as infinitely small and ${{v}_{x}}$ is the velocity component with $x$ as $\cos \theta$ and $\sin \theta$.

Complete step by step solution:
The mass of the train is given as M
The length of the train can be taken as $\dfrac{\pi r}{2}$
Now, we know the mass and the length the train travels therefore, the mass per unit length of the train $\lambda$ is the result of mass divided by the length of the train as:
$\lambda =\dfrac{M}{\dfrac{\pi r}{2}}$
$\Rightarrow \lambda =\dfrac{2M}{\pi r}$
Now let us put the mass of the train as an infinitely small mass where it is denoted as dm.
And with the mass taken as infinitely small, the length is also taken as infinitely small as
$dl\text{ }=\text{ }Rd\theta$
Thereby, placing the values of mass in terms of mass per unit length with the velocity component directing inwards due to linear momentum of centripetal force which is directed inwards as well.
$\text{ }dm\text{ }=\text{ }\dfrac{M}{\pi R\text{ }}Rd\theta$
Placing the value of dm as $\dfrac{M}{\pi R\text{ }}Rd\theta$ in $P=\int{dm{{v}_{x}}}$ with ${{v}_{x}}\ as \[v\sin \theta$ as the work done by a centripetal force is directed inwards as shown in the diagram below:

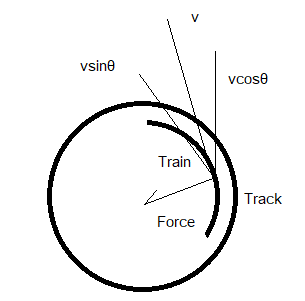
The linear momentum is given as:
$P=\int{\dfrac{M}{\pi R\text{ }}Rd\theta v\sin \theta }$
$\Rightarrow P=\int{\dfrac{M}{\pi R\text{ }}Rd\theta v\sin \theta }$
$\Rightarrow P=\dfrac{Mv}{\pi \text{ }}\int{\sin \theta d\theta }$
Integrating the RHS from zero to $\pi$.
$\Rightarrow P=\dfrac{Mv}{\pi \text{ }}\int{\sin \theta d\theta }$
$\Rightarrow P=\dfrac{Mv}{\pi \text{ }}\left( \cos \pi -\cos 0 \right)$
$\Rightarrow P=\dfrac{2Mv}{\pi \text{ }}$

Therefore, the linear momentum of the train is $\dfrac{2Mv}{\pi \text{ }}$.

Note: The linear momentum follows the second law of Newton's law of motion where the net force acting on the particle is in the direction of the motion and the velocity is changing with time even though the speed remains the same.