Solveeit Logo
Login

Question

Question: A train is running at \(20\,m/s\) on a railway line with a radius of curvature 40,000 meters. The di...

A train is running at 20 m/s20\,m/s on a railway line with a radius of curvature 40,000 meters. The distance between the two rails is 1.5 meters. For safe running of train the elevation of outer rail over the inner rail is
A. 2⋅0 mm2 \cdot 0\,mm
B. 1⋅75 mm1 \cdot 75\,mm
C. 1⋅50 mm1 \cdot 50\,mm
D. 1⋅25 mm1 \cdot 25\,mm

Explanation

Solution

We know the concept of banking of roads when there is a curved path. Same concept is used here in order to provide a safe turn. The formula for finding the angle of elevation is
tan⁡ θ=v2rg\tan \,\theta = \dfrac{{{v^2}}}{{rg}}
Where v is a velocity and g is acceleration due to gravity and r is the radius of curvature.
Tan of an angle can also be found by taking the ratio of opposite side to adjacent side.
tan⁡θ=opposite sideadjacent side\tan \theta = \dfrac{{{\text{opposite}}\,{\text{side}}}}{{{\text{adjacent}}\,{\text{side}}}}
Here, opposite side will be the elevation h and adjacent side is the width of the rail d. From this we can calculate the height of elevation.

Complete step-by-step solution:
It is given that the velocity of the train is v=20 m/sv = 20\,m/s
The radius of curvature of the path is given as r=40000 mr = 40000\,m
The distance between the two rails is given as d=1.5 md = 1.5\,m
We need to find the elevation of the outer rail with respect to the inner rail for safe running of the train.
We know the concept of banking of roads in curved paths. The roads are made in such a way that the outer edge is made at an elevation with respect to the inner edge. This is a safety measure. By doing this necessary centripetal force for taking a safe turn can be provided. Similarly, for the safe turning of trains the rails are also constructed such that the outer rail will be at a higher level than the inner rail where the curved path is present.
In such cases the tan of angle of elevation is found out by the formula
tan⁡ θ=v2rg\tan \,\theta = \dfrac{{{v^2}}}{{rg}}
Where v is a velocity and g is acceleration due to gravity and r is the radius of curvature.
By substituting the values we get tan⁡θ\tan \theta as
tan⁡ θ=(20 m/s)240000 m×10 m/s2\tan \,\theta = \dfrac{{{{\left( {20\,m/s} \right)}^2}}}{{40000\,m \times 10\,m/{s^2}}}
∴tan⁡θ=1×10−3\therefore \tan \theta = 1 \times {10^{ - 3}}
Tan of an angle can also be found by taking the ratio of opposite side to adjacent side.
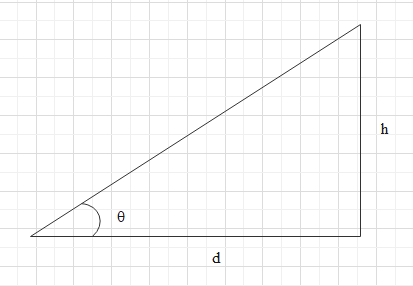
tan⁡θ=opposite sideadjacent side\tan \theta = \dfrac{{{\text{opposite}}\,{\text{side}}}}{{{\text{adjacent}}\,{\text{side}}}}

Here, opposite side will be the elevation h and adjacent side is the width of the rail d.
tan⁡θ=hd\tan \theta = \dfrac{h}{d}
By substituting the value of width of rail in this equation we get
tan⁡θ=h1⋅5\tan \theta = \dfrac{h}{{1 \cdot 5}}
⇒h=1⋅5tan⁡ θ\Rightarrow h = 1 \cdot 5\tan \,\theta
⇒h=1⋅5×10−3 m\Rightarrow h = 1 \cdot 5 \times {10^{ - 3}}\,m
∴h=1.5 mm\therefore h = 1.5\,mm
This is the elevation of the outer rail .
So the correct answer is option C.

Note:- Here we considered the angle of banking without friction. In the absence of friction
tan⁡ θ=v2rg\tan \,\theta = \dfrac{{{v^2}}}{{rg}} Where v is a velocity and g is acceleration due to gravity and r is the radius of curvature.
If friction is involved then the angle of banking with friction is given by the formula
tan⁡ θ+μ1−μtan⁡θ=v2rg\dfrac{{\tan \,\theta + \mu }}{{1 - \mu \tan \theta }} = \dfrac{{{v^2}}}{{rg}}
Where μ\mu represents the coefficient of friction.