Question

A train is moving slowly at 2m/s next to a railway platform. A man, 1.5m tall, alights from the train such that his feet are fixed on the ground. Taking him to be rigid body, the instantaneous angular velocity (in rad/sec) is :
A. 1.5
B. 2.0
C. 2.5
D. 3.0

Answer 1

First draw the diagram as given in the question, now apply the law of conservation of angular momentum, write the formula for the conservation of angular momentum and then put in the values required for the answer.

Formula used:
$mv\dfrac{l}{2}=I\omega$

Complete step-by-step answer:
Here the man is considered as a rigid body, which is fixed at a place,
Now we are applying the law of conservation of angular momentum, about the feet just before and after the landing.

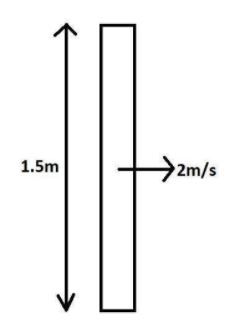
Here in the diagram on the left it is the man 1.5m tall and aligned just to the moving train moving at a velocity of 2m/s.
Now,
$mv\dfrac{l}{2}=I\omega$
$mv\dfrac{l}{2}=\dfrac{M{{L}^{2}}}{3}\omega$,
$\omega =\dfrac{3v}{2l}=\dfrac{3\times 2}{2\times \left( \dfrac{3}{2} \right)}$,
Which gives,
$\omega =2rad/\sec$
Therefore the correct option is option B.

So, the correct answer is “Option B”.

Additional Information: Two examples where we see the phenomenon of conservation of angular momentum is, in aircraft engines and electric generators.
Points to remember when calculating of angular momentum
An object will have no change in angular momentum when it is spinning in a closed system and no external torques are applied to it.
The angular momentum is constant or conserved when the net torque in the body is zero.
Torque is an effect of rotational or twisting of a force. Its SI unit is Nm.

Note: In the formula, $mv\dfrac{l}{2}=\dfrac{M{{L}^{2}}}{3}\omega$, m is the mass, v is the velocity of the train, l is the linear momentum of the body and $\omega$, is the angular momentum. We know that the law of conservation of angular momentum states that no change of angular momentum will occur, when no external torque acts on an object.