Question
Question: A train is moving on a track at \[30{\text{ }}m{s^{ - 1}}\]. A ball is thrown with a speed of \[30{\...
A train is moving on a track at 30 ms−1. A ball is thrown with a speed of 30 ms−1 at 45∘ with horizontal. Find the distance in the plane of motion of the train, of the ball from the point of projection on the train to the point where it strikes the ground.
A) 90 m
B) 903 m
C) 60 m
D) 603m
Solution
1. The motion of the ball is like a motion of a projectile.
2. Determine the horizontal component of the velocity and find the time taken to cover the total path of the projectile motion.
3. Conclude that the total path is the horizontal range of the motion. The range is covered by the ball with a uniform speed. From this concept find the distance between the point of projection and the point where the ball strikes the ground.
4. The frame of reference is the plane of the train.
Formula used:
The horizontal component of the velocity u is, ucosα.
The height of the final point is zero according to the initial point, hence the vertical displacement is zero,
∴0=usinαT−21gT2 [ using the equation of vertical motion, h=ut−21gt2 ]
Where T is the total time taken to cover the whole path of the projectile and g is the gravitational acceleration.
The distance between the initial point and the final point i.e the Horizontal range R=ucosα×T. [using the equation of a uniform velocity, v=ts]
Complete step by step answer:
The ball is thrown at a certain speed at an angle with horizontal. The motion of the ball can be described by a projection. The following diagram defines the motion of the ball inside the train.
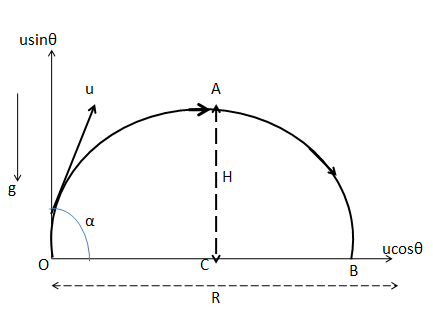
The velocity for the horizontal component u is, ucosα and for the vertical component is usinα. The total time is taken to cover the whole path of the projectile is T.
The height of the final point B is zero according to the initial point O, hence the vertical displacement is zero,
∴0=usinαT−21gT2 [ using the equation of vertical motion, h=ut−21gt2 ]
⇒usinαT=21gT2
⇒usinα=21gT
⇒T=g2usinα
Now, the distance between the initial point O and the final point B i.e OB=R .
The distance between the initial point and the final point i.e the Horizontal range R=ucosα×T [using the equation of a uniform velocity, v=ts ]
∴R=ucosα×g2usinα
⇒R=gu2×2sinαcosα
⇒R=gu2sin2α
Given, u=30m/s
α=45∘
g=9.8m/s2 [known value]
⇒R=9.8302sin(2×45)
⇒R=9.8900
⇒R=91.83
If we take the value of g=10m/s2
Then the value of R=10900=90m
Hence the right answer is in option (A).
Note: The gravitational acceleration g is working downwards. There is no component of g along the horizontal path and so the acceleration is zero. Hence the motion of the ball along the horizontal component is uniform. The frame of reference is the plane of the train. So here the velocity of the train is ignored.
