Question

A train engine that weighs 5000 N stops at the exact centre of a bridge of weight 75,000 N and has two equally spaced pillars to support the bridge. Calculate the upward force exerted by each pillar.
A. 75,000 N
B. 40,000 N
C. 37,500 N
D. 2500 N
E. 0 N

Answer 1

Determine the relation between the normal forces provided by each pillar. Draw the free body diagram of the forces acting on the system. Using Newton's second law in the free body diagram, determine the normal force by each pillar.

Complete Step by Step Answer:
We can see the weight of the train and bridge is balanced by the normal force exerted by the pillars on the horizontal bridge. Let the mass of the bridge is M and the mass of the train is m. Let us draw the situation as shown in the figure below.

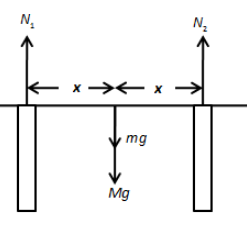
In the above figure, ${N_1}$ is the normal force provided by the first pillar and ${N_2}$ is the normal force provided by the second pillar.

Since the train does not rotate with respect to the centre of mass, we can say the net torque is zero. Let us express the net torque on the system as follows,
${\tau _{net}} = {\tau _1} - {\tau _2} = 0$
$\Rightarrow {N_1}{x_1} - {N_2}{x_2} = 0$
$\Rightarrow {N_1}{x_1} = {N_2}{x_2}$
Here, ${x_1}$ and ${x_2}$ are the distances of the first and second pillars from the train respectively.
Since the train is situated at the exact centre of the bridge, the two distances are equal. Therefore, the above equation becomes,
${N_1} = {N_2}$
Thus, the normal force by both the pillars is the same.

From the free body diagram shown above, we can write,
$2{N_1} = mg + Mg$
$\Rightarrow {N_1} = \dfrac{1}{2}\left( {mg + Mg} \right)$
Substituting $mg = 5000\,{\text{N}}$ and $Mg = 75000\,{\text{N}}$ in the above equation, we get,
${N_1} = \dfrac{1}{2}\left( {5000 + 75000} \right)$
$\therefore {N_1} = 40000\,{\text{N}}$
Therefore, the upward force exerted by each pillar is 40,000 N.

So, the correct answer is option B.

Note: Students should never state that the normal force provided by each pillar is the same without using the net torque on the system is zero. The torque on each side has an opposite direction so that it can rotate. Therefore, we have taken the negative sign for the second torque.