Question

A train A which is $120m$ long is running with velocity $20 m/s$ while train B which is $130 m$ long is running in the opposite direction with velocity $30 m/s$. What is the time taken by train B to cross the train A?
A. $5 s$
B. $25 s$
C. $10 s$
D. $100 s$

Answer 1

The velocity of the train B with respect to train A is the sum of speeds of both the trains. To cross train A, the train B has to move the sum of length of both the trains. Use the relation between distance, velocity and time to determine the time taken by the train B to cross train A.

Formula used:
$v = \dfrac{d}{t}$
Here, v is the velocity, d is the distance and t is the time.

Complete step by step answer:
For the observer standing outside the train will note the speed of the train B is 30 m/s but the observer inside the train A will note the speed of train B far greater than 30 m/s since the direction of motion of these two trains is opposite. Let’s express the speed of train B with respect to train A as,
${v_{BA}} = {v_B} + {v_A}$
Here, ${v_B}$ is the speed of train B and ${v_A}$ is the speed of train A.

Substituting 30 m/s for ${v_B}$ and 20 m/s for ${v_A}$ in the above equation, we get,
${v_{BA}} = 30 + 20$
$\Rightarrow {v_{BA}} = 50\,{\text{m/s}}$

Let’s draw the motion of train A and train B as shown in the figure below.

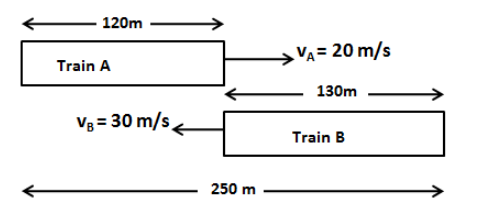
From the above figure, the total distance to be covered by the train B to cross the train A is 250 m.

Let’s use the relation between distance, velocity and time to calculate the time taken by the train B to cross the train A as follows,
$t = \dfrac{d}{{{v_{BA}}}}$
Substituting 250 m for d and 50 m/s for ${v_{BA}}$ in the above equation, we get,
$t = \dfrac{{250}}{{50}}$
$\therefore t = 5\,{\text{s}}$
Therefore, the time taken by train B to cross train A is 5 second.

So, the correct answer is option A.

Note: Do not take the difference in the speeds of the trains to denote the speed of train B with respect to train A. There will be the difference in the speeds of the both trains when the direction of motion of the two trains is the same. To cross train A, the train B has to move the sum of length of both the trains and not just the length of train A.