Question

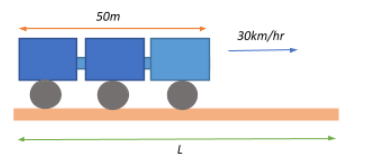
A train 50m long passes over a bridge at a velocity of $30\;kmh^{-1}$. If it takes $36\;s$ to cross the bridge, what will be the length of the bridge?

Answer 1

We are given with the velocity of the train and the time it takes to cross the bridge, so the distance the train travels will be the product of the velocity and time taken. However, remember to account for the length of the train when you take the distance travelled since the engine will have to travel an additional 50m so that the whole train crosses the bridge.

Formula Used:
Distance travelled $d = velocity \times time$

Complete answer:
Let us take the length of the bridge to be $L$.
If the whole train has to cross the bridge, then the distance (d) covered by the engine for the whole train to cross the bridge will be $d = (L+50)\;m = (L+0.05)\;km$
Given that the velocity of the train is $v = 30\;kmh^{-1}$ and it takes $t=36\;s = \dfrac{36}{3600} = 0.01\;h$ to travel, the distance travelled by the train is given by:
$distance = velocity\times time \Rightarrow d = v \times t$
$\Rightarrow (L+ 0.05) = 30 \times 0.01$
$\Rightarrow (L +0.05) = 0.3$
$\Rightarrow L = 0.3-0.05=0.25\;km = 250\;m$
Therefore, the length of this bridge is 250m.

Note:
Instead of converting all the other parameters to make them consistent with the units of the speed, you can in fact just change the unit of speed to save time. To convert a speed from $kmh^{-1}$ to $ms^{-1}$ just multiply the speed in $kmh^{-1}$ by a factor of $\dfrac{5}{18}$, and to convert $ms^{-1}$ to $kmh^{-1}$ multiple the speed by a factor of $\dfrac{18}{5}$.