Question

(a) Trace the path of the ray through the prism.

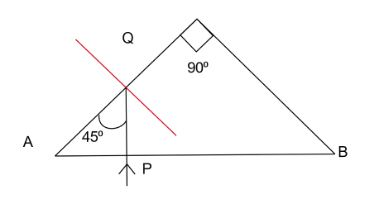
(b) What will be the effect on the path of the ray if the refractive index of the prism is $1.4$ ?

Answer 1

We are asked two things; one is to complete the diagram of the prism and the second one is to explain the effect of the refractive index on the ray of light. We can start by completing the diagram. Then we can move onto the second part. Both solutions will be dependent on the Fermat’s principle which is also known as the principle of least time.

Formulas used:
The formula for critical angle is given as,
$\sin {\theta _c} = \dfrac{1}{\mu }$
Where $\mu$ is the refractive index of the medium.

Complete step by step answer:
(a)
The red lines are normal to each surface.

(b) The value of the refractive index of the prism is given as, $1.4$. Using the formula,
$\sin {\theta _c} = \dfrac{1}{\mu }$
If the value of critical angle is greater than the critical angle, then total internal reflection happens. Substituting the values, we get
$\sin {\theta _c} = \dfrac{1}{\mu } = \dfrac{1}{{1.4}} = 0.71$
Now we can find the angle by taking the sine inverse function on both the sides, by doing this we get
${\sin ^{ - 1}}\left( {\sin {\theta _c}} \right) = {\sin ^{ - 1}}\left( {0.71} \right)$
The value we get will be like ${\theta _c} = 45.58$. We can see that this value is greater than the incident angle and hence total internal reflection does not occur.

Note: Total internal reflection is a process by which all of the incident light gets reflected when the rays of light come in contact with a denser medium. The condition for total internal reflection is that the incident angle must be greater than the critical angle.Critical angle is the angle at which the angle of refraction is ninety. Total internal reflection or TIR has a number of applications including in many optical instruments like the telescope and microscope.