Question

A toy plane P starts flying from point A along a straight horizontal line $20\;m$ above ground level starting with zero initial velocity and acceleration $2\;ms^{-2}$ as shown. At the same instant, a man throws a ball vertically upwards with initial velocity ‘u’. The ball touches (coming to rest) the base of the plane at point B of the plane's journey when it is vertically above the man. ‘s’ is the distance of point B from point A. Just after contact of the ball with the plane, the acceleration of the plane increases to $4\;ms^{-2}$.

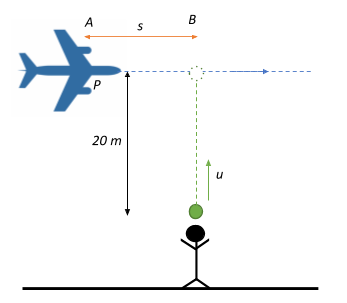
Find:
i) Initial velocity of the ball
ii) Distance ‘s’
iii) Distance between the man and the plane when the man catches the ball back. ($g=10\;ms^{-2}$) (Neglect the height of the man).

Answer 1

For the first part, account for the acceleration due to gravity acting on a ball as a result of its projected vertically upwards. Use the equation of motion correlating the initial velocity, final velocity, acceleration and height travelled, to arrive at the appropriate result.
For the second part, first determine the time that the ball takes to reach the base of the plane at B, which you can use as the time taken by the plane to travel distances, following which you can plug in this value in another equation of motion to arrive at the distance s travelled by the plane.
For the final part, determine the horizontal distance that the plane travels till the ball reaches the man and use Pythagoras theorem for a right-angled triangle to arrive at the distance between the plan and the man at that instant. Note that the time of ascent is the same as the time of descent for a vertically projected body.

Formula Used:
$v=u+at$
$s=ut+\dfrac{1}{2}ga^2$
$v^2=u^2+2as$

Complete Solution Step-by-Step:
We are given that the initial velocity of the plane is $u_{p} = 0\;ms^{-1}$, the initial acceleration of the plane $a_i = 2\;ms^{-2}$, and final acceleration of the plane after contact with the ball is $a_f = 3\;ms^{-2}$ after travelling a distance s. The plane is at a height $h=20\;m$.

Let the initial velocity of the ball be $u_b$, and let the acceleration due to gravity acting on the ball be $g\approx 10\;ms^{-2}$

i) We are required to find the initial velocity with which the ball is projected.
When the ball comes in contact with the base of the plane at B it comes to a momentary stop, i.e., $v_b = 0$ at B. We know that the ball travels vertically upwards through a distance of $h=20\;m$, so the acceleration on the ball is entirely gravitational and since the motion of the ball is opposite to the gravitational force, it possesses a negative sign, i.e., $a=-g$.

We can determine the initial velocity of the ball by plugging in the above values in the following equation of motion:
$v^2_b=u^2_b -2gh \Rightarrow 0 = u^2_b – (2\times 10\times 20)$
$\Rightarrow u^2_b = 400 \Rightarrow u_b=\sqrt{400} \Rightarrow u_b = 20\;ms^{-1}$

Therefore, the initial velocity of the ball is $20\;ms^{-1}$.

ii) We are now required to find the distance “s” travelled by the plane between points A and B.
We know that the time taken by the plane to travel the distance s is the time taken for the ball to make contact with the base of the plane, which we find to be,
$v_b = u_b -gt \Rightarrow 0 = 20 -10(t) \Rightarrow t=\dfrac{20}{10} = 2\;s$

Therefore, for the plane, the distance it travels in this time can be calculated as:
$s=u_pt+\dfrac{1}{2}a_it^2 = 0+\dfrac{1}{2}\times 2\times 2^2 = 4\;m$

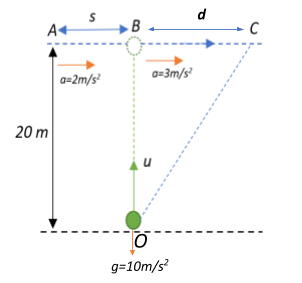
iii) We finally find the distance between the man and the plane when he catches the ball back. This distance is given as OC in the diagram.
Now, the time taken by the ball to reach the ground is the same as the time taken by the ball to reach the base of the plane, i.e., $t=2\;s$

At point B, the velocity of the plane can be found to be:
$v_p = u_p+a_it = 0 + (2\times 2) = 4\;ms^{-1}$

If the acceleration of the plane from points B to C is $a_f=3\;ms^{-2}$, the distance travelled by the plane from B to C can be calculated as:
$BC = v_pt + \dfrac{1}{2}a_ft^2 = (4\times 2) + \dfrac{1}{2}\times 3\times 2^2 = 8+6 = 14\;m$.

Consider the right angled $\triangle OBC$. We can find OC by using Pythagoras theorem:
$OC^2=OB^2+BC^2 \Rightarrow OC = \sqrt{OB^2+BC^2}$
$\Rightarrow OC = \sqrt{20^2+14^2} = \sqrt{400+196} = \sqrt{596} = 24.4\;m$

Therefore, the distance between the man and the plane after he catches the ball is $24.4\;m$

Note:
When the problem has equations of motion related to two bodies, it is important to remember not to mix up the equations and the parameters (defined or calculated) between them. Doing so will result in inconsistent solutions, which can be avoided if careful attention is paid to them. As in the case above, if you are defining an equation of motion for the ball (plane), ensure that the parameters plugged in are all defined for the ball (plane), unless explicitly specified or logically deduced that they are interchangeable.