Question

A toy car with charge q moves on a frictionless horizontal plane surface under the influence of a uniform electric field $\overrightarrow E$, Due to the force $q\overrightarrow E$, its velocity increases from 0 to 6 m/s in one-second duration. At that instant, the direction of the field is reversed. The average velocity and the average speed of the toy car between 0 to 3 seconds are respectively.
A. $1m/s,3.5m/s$
B. $2m/s,4m/s$
C. $1.5m/s,3m/s$
D. $1m/s,3m/s$

Answer 1

Here, the toy car is moving under the influence of the electrostatic force, which accelerates the car. This acceleration can be found by using the first equation of motion. Using the acceleration we can find the velocity of the car which helps in plotting the v-t graph. From the graph, one can calculate the average velocity and the average speed.
Formula used:
\eqalign{ & v = u + at \cr & {\overline v _{avg}} = \dfrac{{{s_{total}}}}{t} = \dfrac{{area}}{t} \cr & {v_{avg}} = \dfrac{{{d_{total}}}}{t} = \dfrac{{\left| {area} \right|}}{t} \cr}

Complete step-by-step solution:
Consider the given situation. Initially, the car with charge q has been moving under the influence of some electric field $\overrightarrow E$. This force $q\overrightarrow E$ causes some acceleration, say a. This acceleration is given by the first equation of motion which is
$v = u + at$
Where,
v is the final velocity of the object
u is the initial velocity of the object
a is the acceleration
t is the time taken
In time $0 < t < 1s$, the velocity increases from 0 to 6m/s. So, the acceleration of the object in the first second will be
\eqalign{ & v = u + at \cr & \Rightarrow 6 = 0 + a \times 1 \cr & \Rightarrow a = 6m/{s^2} \cr}
In the time interval $1s < t < 2s$, the field has changed its direction. The final velocity in the last interval will be the initial velocity. And the toy car will decelerate until it reaches zero. This deceleration will be the same as the initial acceleration but in the opposite direction. The final velocity will be is given by
\eqalign{ & {v_2} = {v_1} + \left( { - a} \right)t \cr & \Rightarrow {v_2} = 6 - a \times \left( {2 - 1} \right) \cr & \Rightarrow {v_2} = 6 - 6 \cr & \Rightarrow {v_2} = 0 \cr}
The negative symbol indicates that the car is decelerating.
In the next time interval $2s < t < 3s$, the toy car will now accelerate in the direction of the field, as it is aligned with the field. If we say that the acceleration of the car in this time interval is the same as before, then the final velocity is given by
\eqalign{ & {v_3} = {v_2} + \left( { - a} \right)t \cr & \Rightarrow {v_3} = 0 - a \times \left( {3 - 2} \right) \cr & \Rightarrow {v_3} = - 6m/s \cr}
Now, if we plot a graph of v-t, it will look something like this

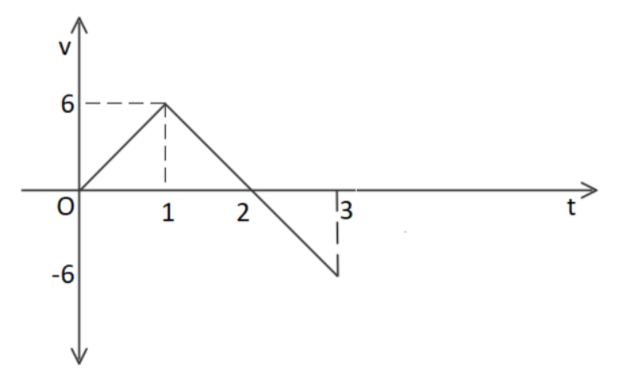
The average velocity of the graph will be given by the ratio of the total displacement to the total time interval. The total displacement will be given by the area under the curve. That is
\eqalign{ & {\overline v _{avg}} = \dfrac{{{s_{total}}}}{t} = \dfrac{{area}}{t} \cr & \Rightarrow {\overline v _{avg}} = \dfrac{{\dfrac{1}{2} \times 2 \times 6 + \dfrac{1}{2} \times 1 \times - 6}}{3} \cr & \Rightarrow {\overline v _{avg}} = \dfrac{{6 - 3}}{3} \cr & \Rightarrow {\overline v _{avg}} = 1m/s \cr}
Similarly, the average speed is denoted by
\eqalign{ & {v_{avg}} = \dfrac{{{d_{total}}}}{t} = \dfrac{{\left| {area} \right|}}{t} \cr & \Rightarrow {v_{avg}} = \dfrac{{\left| {\dfrac{1}{2} \times 2 \times 6} \right| + \left| {\dfrac{1}{2} \times 1 \times - 6} \right|}}{3} \cr & \Rightarrow {v_{avg}} = \dfrac{{6 + 3}}{3} \cr & \Rightarrow {v_{avg}} = 3m/s \cr}
Therefore, the average velocity is 1m/s and the average speed is 3m/s.
Thus, the correct option is D.

Note: The equations of motion only apply to objects having constant acceleration. The velocity of an object is a vector whereas the speed is a scalar. That is the reason why we don’t consider the negative sign of the area for calculating distance which is also a scalar, in contrast to displacement.