Question

A Toy car starts from rest at position 1 shown in figure and moves without the friction along the loop 12324:-

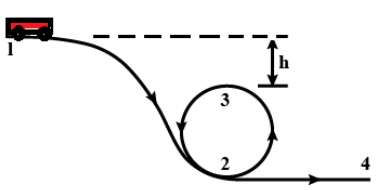
A. The smallest height h at which the car can negotiate without falling off the track is $\dfrac{r}{2}$
B. If the car just negotiates the loop, the speed of car at position 4 is $\sqrt{5r}$
C. If the car just negotiates the loop, the speed of car at position 2 is 6 mg
D. If the car just negotiates the loop, the speed of car at position 3 is $ma$

Answer 1

Before proceeding with the solution, we must get through with the principle of conservation of mechanical energy as it is the key part of the approach of finding the solution.
The principle of the conservation of mechanical energy states that the total mechanical energy in a system (i.e., the sum of potential and kinetic energies) remains constant as long as the only forces acting are conservative forces i.e. the value of mechanical energy does not equal to zero ever.
The principle of the conservation of mechanical energy would help us in proceeding with the solution of the given question as the gravitational energy of the car would be balanced by centrifugal force and thus, equating them would get us the correct solution.

Complete answer:
Let ‘m’ be the mass of the toy car.
Let ‘g’ be the acceleration on the toy car due to gravity.
Let ‘r’ be the radius of the circular track.
Let ‘h’ be the difference in height between position 1 and position 3 of the track.
It is given that the track is frictionless.
For the critical value of h, the car will lose its contact with the track at position 3 due to which the normal reaction ceases to exist.
As a result, the gravitational force gets balanced by centrifugal force.
i.e. $mg={{\dfrac{mv}{r}}^{2}}$
As per the Law of Conservation of Mechanical Energy,
$\Rightarrow \text{Total energy at position 1 = Total energy at position 3}$
$\Rightarrow mgh=\dfrac{1}{2}m{{v}^{2}}$
$\Rightarrow$ $h=\dfrac{{{v}^{2}}}{2g}$
$\Rightarrow$ $h=\dfrac{rg}{2g}$
$\Rightarrow h=\dfrac{r}{2}$

Hence the correct option would be option (A). The smallest height h at which the car can negotiate without falling off the track is $\dfrac{r}{2}$ .

Note:
While using the Law of conservation of mechanical energy, one must keep in mind that potential energy is equal to the kinetic energy of the object only if the object travels from a height h to $h=0$. And also, proper conversion of the unit must also be taken care of when required.