Question

A tower ${\text{51mts}}$ high has a mark at a height of ${\text{25mts}}$ from the ground. At what distance do the two parts subtend equal angle to an eye at the height of ${\text{5mts}}$ from the ground?
A) 20 mts
B) 30 mts
C) 15 mts
D) 160 mts

Answer 1

In this question we will simplify this by using diagram. We have to divide 51 mts in two parts of 25 mts and 26 mts. Then by using angle bisector property we can find the height.

Complete step-by-step answer:
The diagram will be as follows:
Given data is:
AC =51 mts , which is being divided as,
AD = 5mts
AB = 25 mts
So, BC = 26 mts
Also, PQ = 5 mts.

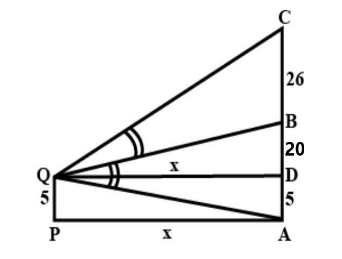
AC is the tower of height 51 mts. Point B is at 25 mts from the ground. Let us assume that distance QD is x mts.
From the diagram and the question we have been given that,
$\angle CQB = \angle AQB$
$\therefore$QB is the bisector of angle AQC. And as such it divides the base AC in the ratio of the arms of the angle, according the geometry, we have
$\dfrac{{AB}}{{BC}} = \dfrac{{QA}}{{QC}}$
Now, we will find QA value by using Pythagoras theorem in $\vartriangle QAD$ ,
$Q{A^2} = Q{D^2} + D{A^2} \\\ \Rightarrow QA = \sqrt {Q{D^2} + D{A^{}}} \\\$ ….(1)
Similarly, we will find QC value by using Pythagoras theorem in $\vartriangle QCD$ ,
$Q{C^2} = Q{D^2} + D{C^2} \\\ \Rightarrow QC = \sqrt {Q{D^2} + D{C^2}} \\\$ ….(2)
So, from equations 1 and 2 , we have from the diagram,
Or $\dfrac{{25}}{{26}} = \dfrac{{\sqrt {Q{D^2} + D{A^2}} }}{{\sqrt {Q{D^2} + D{C^2}} }}$ …(3)
Substitute the values of DA , DC AND QD from the diagram in equation 3,
$\dfrac{{25}}{{26}} = \dfrac{{\sqrt {{x^2} + {5^2}} }}{{\sqrt {{x^2} + {{46}^2}} }}$
Squaring on both the sides, we get,
$625\left( {{x^2} + {{46}^2}} \right) = 676\left( {{x^2} + 25} \right)$
Now, we will do simplification of the above expression as,
$51{x^2} = \left( {625 \times {{46}^2} - 676 \times 25} \right) \\\ {x^2} = \dfrac{{100\left[ {13225 - 169} \right]}}{{51}} \\\ {x^2} = 100 \times \dfrac{{13056}}{{51}} \\\ \Rightarrow 100 \times 256 \\\ \Rightarrow x = 10 \times 16 = 160m \\\$
x = 160 mts

$\therefore$ The distance between the two parts will be 160 mts.

Note: This problem can be solve by using $\tan \theta$ property, in this we will take angle $\angle QCB = \angle QBD = \alpha$ and $\angle QAD = \theta$ so that first we will calculate $\tan \theta$ then $\tan \left( {\alpha - \theta } \right)$ then $\tan \left( {2\alpha - \theta } \right)$ and after that find all three values and make equation in form of height and calculate it.