Question

A tower stands vertically on the ground. From a point on the ground which is 30m away from the foot of the tower, the angle of elevation of the top of the tower is found to be ${45^ \circ }$ . Find the height of the tower.
A. 15
B. 40
C. 30
D. 20

Answer 1

Hint: This is a problem based on the application of trigonometry. In these types of problems, it is necessary to draw a diagram and then observe what we are told to find and what we are already given. Then we have to use the concept of trigonometric ratios. Here we will use $\tan \theta = \dfrac{{Perpendicular}}{{Base}}$

Complete step-by-step answer:
Let us try to draw the figure as discussed in the question,

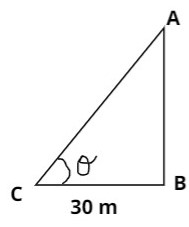
Here BC is the distance from the point of elevation C to the tower located at point B,
The height of the tower is AP which is also the perpendicular in the right-angled triangle ABC
Here $\theta$ is the point of elevation and according to the question $\theta = {45^ \circ }$ Now as we are told to find the value of height of tower which is also the perpendicular and we are given the base and the angle of elevation. It is best to use trigonometric function named tangent which is also equals to $\dfrac{{Perpendicular}}{{Base}}$
So as we know that

\therefore \tan \theta = \dfrac{{Perpendicular}}{{Base}}\\\ \Rightarrow \tan {45^ \circ } = \dfrac{{Perpendicular}}{{30}}\\\ \Rightarrow 1 = \dfrac{{Perpendicular}}{{30}}\\\ \Rightarrow Perpendicular = 30 \end{array}$$ So now we have the height of the tower as 30 meters Therefore option C is the correct option here. Note: It must be noted that $$\tan {45^ \circ } = \tan \dfrac{\pi }{4} = 1$$ which is used in the solution also it is necessary to choose the trigonometric functions wisely in these type of questions as we must know along with the angle which side is given and which is told to find to pair up correctly because we only want one variable in our equation to solve it easily.