Solveeit Logo
Login

Question

Question: A tower of height ′ h ′ standing vertically at the center of a square f side length ′ a ′ subtends t...

A tower of height ′ h ′ standing vertically at the center of a square f side length ′ a ′ subtends the same angle ′ θ ′ at all the corner points of the square. Then
A 2h2=a2tan⁡2θ2{h^2} = {a^2}{\tan ^2}\theta
B a2=2h2tan⁡2θ{a^2} = 2{h^2}{\tan ^2}\theta
C a2=2h2cot⁡2θ{a^2} = 2{h^2}{\cot ^2}\theta
D 2a2=h2cot⁡2θ2{a^2} = {h^2}{\cot ^2}\theta

Explanation

Solution

Hint : Height is the measurement of an object in the vertical direction and distance is the measurement of an object from a particular point in the horizontal direction and a right-angled triangle is used to calculate heights and distances. The height of an object is calculated by measuring the distance from the object and the angle of elevation of the top of the object. The tangent of the angle is the object height divided by the distance from the object. Thus, the height is found.

Complete step-by-step answer :
Here, ae some of the points you must know while dealing with heights and distances:
The line which is drawn from the eyes of the observer to the point being viewed on the object is known as the line of sight.
The angle of elevation of the point on the object (above horizontal level) viewed by the observer is the angle which is formed by the line of sight with the horizontal level.
The angle of depression of the point on the object (below horizontal level) viewed by the observer is the angle which is formed by the line of sight with the horizontal level.

′ h ′ standing vertically at the center of a square f side length ′ a ' subtends the same angle ′ θ ′ at all the corner points of the square which is represented as:

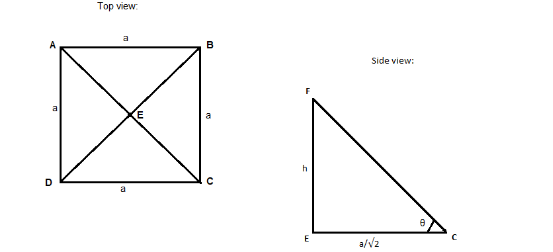
In, ΔEFC\Delta EFC
tan⁡θ=EFEC\tan \theta = \dfrac{{EF}}{{EC}}
tan⁡θ=EFEC=ha2\tan \theta = \dfrac{{EF}}{{EC}} = \dfrac{h}{{\dfrac{a}{{\sqrt 2 }}}}
\Rightarrow $$$$\dfrac{a}{{\sqrt 2 }}\tan \theta = h
\Rightarrow $$$$a\tan \theta = \sqrt 2 h
Squaring both sides, we get
\Rightarrow $$$$2{h^2} = {a^2}{\tan ^2}\theta
So, the correct answer is “Option C”.

Note : The calculation of the height of an object is achieved by the measurement of its distance from the object. This includes the angle of elevation at the top of the object while calculating the height. The tangent of the angle is considered as the height of the object, which is divided by the distance from the object.