Question

A tower has obtained two stations A and B where B is East of A at a distances 100 meters. The tower is due North of A and due North-West of B. The angles of elevation of the tower from A and B are complementary. Find the height of the tower.

Answer 1

Hint : We will use the Pythagoras theorem to find the unknown sides which states that
${P^2} + {B^2} = {H^2}$
Where, $P$ is the perpendicular, $B$ is the base and $H$ is the hypotenuse of the triangle.
We will find the angles in the different right-angled triangles and then find their product to find the height of the tower.

Complete step-by-step answer :
We will assume the height of the tower $PQ$ be $h$ .
Now we will assume station $A$ and station B to be as the point of observation.
It is given in the question that station $B$ is in the northwest of station $A$ .
Also point $Q$ of the tower is in the due north of station $A$ . The following is the schematic diagram of the tower.

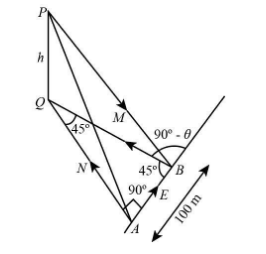
It is clear from the diagram that angle $\angle QAP = {90^ \circ }$ and $\angle QBA = {45^ \circ }$ .
Now we will consider the triangle $\Delta QAB$ , in which,
We have $\angle QAB = {90^ \circ }$ and $\angle QBA = {45^ \circ }$ . Also we know that $QA = AB = 100\;{\rm{m}}$ .
Hence, the triangle $\Delta QAB$ is a right-angled triangle. Therefore, we can apply Pythagoras theorem in it which states that,
${P^2} + {B^2} = {H^2}$
Where, $P$ is the perpendicular, $B$ is the base and $H$ is the hypotenuse of the triangle.
Now we will substitute $100\;{\rm{m}}$ for $P$ and $100\;{\rm{m}}$ for $B$ in the above expression to find $H$ .

{H^2} = {\left( {100\;{\rm{m}}} \right)^2} + {\left( {100\;{\rm{m}}} \right)^2}\\\ {H^2} = 2{\left( {100\;{\rm{m}}} \right)^2}\\\ H = 100\sqrt 2 \;{\rm{m}} \end{array}$$ Therefore, $ QB $ is equal to $ 100\sqrt 2 \;{\rm{m}} $ . Now we will consider another right-angled triangle $ \Delta AQP $ . $ \cot \theta = \dfrac{{AQ}}{h} $ Rearranging the above expression, we get, $ AQ = h\cot \theta $ We will substitute $ 100\;{\rm{m}} $ for $ AQ $ in the above expression. $$100\;{\rm{m}} = h\cot \theta $$ ……(i) Now we will consider another right-angled triangle $ \Delta BQP $ . $ \cot \left( {{{90}^ \circ } - \theta } \right) = \dfrac{{QB}}{h} $ Rearranging the above expression and also substituting $ \tan \theta $ for $ \cot \left( {{{90}^ \circ } - \theta } \right) $ , we get, $ QB = h\tan \theta $ Now we will substitute $ 100\sqrt 2 \;{\rm{m}} $ for $ QB $ in the above expression. $ 100\sqrt 2 \;{\rm{m}} = h\tan \theta $ ……(ii) Now we multiply equation (i) with (ii), we will get, $$100\;{\rm{m}} \times 100\sqrt 2 \;{\rm{m}} = h\cot \theta \times h\tan \theta $$ Rearranging the above expression, and substituting $ \cot \theta \times \tan \theta $ for 1 we will get, $$\begin{array}{l} {h^2} = 100\;{\rm{m}} \times {\rm{100}}\sqrt {\rm{2}} \;{\rm{m}}\\\ h = 100{\left( 2 \right)^{\dfrac{1}{4}}}\;{\rm{m}}\\\ h = 118.92\;{\rm{m}} \end{array}$$ Hence the value of $ h $ is $ 118.92\;{\rm{m}} $ . **Note** : In such types of problems, always make sure to find the values of different angles in the different right-angled triangles carefully. Also we have to use the trigonometric properties to simplify the question.