Solveeit Logo
Login

Question

Question: A tower 51mts high has a mark at a height of \[25\] mts from the ground. At what distance the two pa...

A tower 51mts high has a mark at a height of 2525 mts from the ground. At what distance the two parts subtend equal angle to an eye at the height of 55 mts from the ground
A. 20mts20mts
B. 30mts30mts
C. 15mts15mts
D. 160mts160mts

Explanation

Solution

Hint : We will make a given diagram according to the given information in the question .Then we will take two triangles separately and find a side by using Pythagora's theorem.

Complete step-by-step answer :

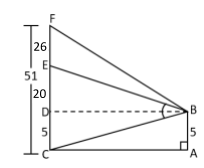
Here, CFCF is the height of the tower and it has a mark at height of 2525meters from the ground.
AB=CD=5 meters,  DE=2 metersAB = CD = 5\,meters,\,\,DE = 2\,meters
DE=EC−CD DE=25−5 DE=20meters  DE = EC - CD \\\ DE = 25 - 5 \\\ DE = 20meters \\\
CF=51 metersCF = 51\,meters
DF=DE+EF DF=20+26 DF=46meters  DF = DE + EF \\\ DF = 20 + 26 \\\ DF = 46meters \\\
Now, according to the question:
∠FBE=∠EBC\angle FBE = \angle EBC (∵\because given)
∴BE\therefore BE is the bisector of ∠CBF\angle CBF and as such it divides the base CFCF in the ratio of the arm of the angle. Then by the angle bisector theorem .
BCBF=CEEF\dfrac{{BC}}{{BF}} = \dfrac{{CE}}{{EF}} …..(i)
Now, In ΔBDE,\Delta BDE, at point D=90oD = {90^o}
By using Pythagoras theorem, we have
(Hypotenuse)2 = (base)2+(perpendicular)2
(BF)2=(BD)2+(DF)2{(BF)^2} = {(BD)^2} + {(DF)^2}
(BF)2=(BD)2+(DF)2{(BF)^2} = {(BD)^2} + {(DF)^2}
We will substitute the value of DF,DF=46DF = 46
(BF)2=(BD)2+(46)2 ⇒BF=(D)2+(46)2  {(BF)^2} = {(BD)^2} + {(46)^2} \\\ \Rightarrow BF = \sqrt {{{(D)}^2} + {{(46)}^2}} \\\
In ΔBCD\Delta BCDat point Dis9090, so by using Pythagoras theorem, we have
(Hypotenuse)2 = (base)2+(perpendicular)2
(BC)2=(BD)2+(DC)2{(BC)^2} = {(BD)^2} + {(DC)^2}
BC=(BD)2+(DC)2BC = \sqrt {{{(BD)}^2} + {{(DC)}^2}}
We will substitute the value of DC,DC=5DC = 5
BC=(BD)2+(5)2BC = \sqrt {{{(BD)}^2} + {{(5)}^2}}
Now, we will put the value of BFBFand BCBC in equation (i) ,we have
(BD)2+(5)2(BD)2+(46)2=CEEF\dfrac{{\sqrt {{{(BD)}^2} + {{(5)}^2}} }}{{\sqrt {{{(BD)}^2} + {{(46)}^2}} }} = \dfrac{{CE}}{{EF}}
Squaring both sides, we will get
((BD)2+(5)2)2((BD)2+(46)2)2=(CEEF)2\dfrac{{{{\left( {\sqrt {{{(BD)}^2} + {{(5)}^2}} } \right)}^2}}}{{{{\left( {\sqrt {{{(BD)}^2} + {{(46)}^2}} } \right)}^2}}} = {\left( {\dfrac{{CE}}{{EF}}} \right)^2}
(BD)2+(5)2(BD)2+(46)2=(2526)2\dfrac{{{{(BD)}^2} + {{(5)}^2}}}{{{{(BD)}^2} + {{(46)}^2}}} = {\left( {\dfrac{{25}}{{26}}} \right)^2}
(BD)2+25(BD)2+2116=625676\dfrac{{{{(BD)}^2} + 25}}{{{{(BD)}^2} + 2116}} = \dfrac{{625}}{{676}}
676[(BD)2+25]=625[(BD)2+2116]676[{(BD)^2} + 25] = 625[{(BD)^2} + 2116]
We will equate the values of (BD)2{(BD)^2}, we have
676(BD)2+676×25=625×(BD)2+625×2116676{(BD)^2} + 676 \times 25 = 625 \times {(BD)^2} + 625 \times 2116
676(BD)2−625(BD)2=625×2116−676×25676{(BD)^2} - 625{(BD)^2} = 625 \times 2116 - 676 \times 25
(672−625)(BD)2=25(25×2116−676)(672 - 625){(BD)^2} = 25(25 \times 2116 - 676)
51(BD)2=25×4(25×529−169)51{(BD)^2} = 25 \times 4(25 \times 529 - 169)
51(BD)2=100(13225−169)51{(BD)^2} = 100(13225 - 169)
51(BD)2=100(13056)51{(BD)^2} = 100(13056)
(BD)2=100×1305651{(BD)^2} = \dfrac{{100 \times 13056}}{{51}}
(BD)2=100×256{(BD)^2} = 100 \times 256 …..(ii)
256=2×2×2×2×2×2×2×2256 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2
256=(2×2×2×2)2256 = {(2 \times 2 \times 2 \times 2)^2}
256=(16)2256 = {(16)^2}
Now, we will substitute the value of 256256 in equation (ii) , we have
So, (BD)2=100×(16)2{(BD)^2} = 100 \times {(16)^2}
(BD)2=(10)2×(16)2{(BD)^2} = {(10)^2} \times {(16)^2}
(BD)2=(10×16)2{(BD)^2} = {(10 \times 16)^2}
So, BD=(10×16)2BD = \sqrt {{{(10 \times 16)}^2}}
BD=160BD = 160meters
Hence, the required answer is 160 meters.

Note : Students must know that an angle bisector divides the angle into two angles with equal measures. We will find the value of BD with the help of Pythagoras theorem.