Question

A total charge $Q$ is distributed uniformly into a spherical volume of radius $R$. Find the electrostatic energy of this configuration.
(A) $\dfrac{{{Q^2}}}{{4\pi {\varepsilon _0}R}}$
(B) $\dfrac{{3{Q^2}}}{{5\pi {\varepsilon _0}R}}$
(C) $\dfrac{{3{Q^2}}}{{20\pi {\varepsilon _0}R}}$
(D) $\dfrac{{3{Q^2}}}{{10\pi {\varepsilon _0}R}}$

Answer 1

The work done in bringing 2 charges ${q_1}$ and ${q_2}$ which are separated by a distance of ${r_{12}}$ is given by $W = \dfrac{{{q_1}{q_2}}}{{4\pi {\varepsilon _0}{r_{12}}}}$. By principle of superposition we could estimate the total electrostatic energy needed to bring together a sphere of radius $R$.

Formulas used: We will be using the formula $W = \dfrac{{{q_1}{q_2}}}{{4\pi {\varepsilon _0}{r_{12}}}}$ where $W$ is the work done in bringing together two charges ${q_1}$ and ${q_2}$ from a distance of ${r_{12}}$ between each other. We will also be using some of the basic integration and differentiation techniques.

Complete Step by Step answer
The law of conservation of energy is one of the most used and important laws of mechanics and kinetics. It helps find the state of the particle without knowing its path. This principle can be used in electrostatics as well. However, here we might call it electrostatic energy.
So let us consider a sphere of radius $R$ and total charge $Q$ . Also consider an infinitesimally small ring within the sphere which is away from the centre by $r$ units. Let us consider that the thickness of the ring is $dr$ . Also consider a charge $dQ$ which is at a distance $a$ from the centre of the sphere.

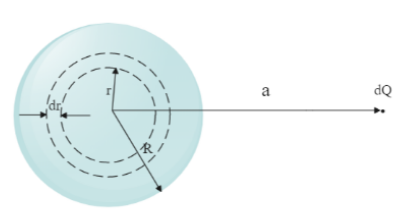
Now let us find the work that should be done to bring the charge $dQ$ to the ring $rdr$ .
$dU = \dfrac{{QdQ}}{{4\pi {\varepsilon _0}r}}$
If the density of the charge in the sphere is $\rho$ then we can write $Q = \rho \times V$ where $V$ is volume of the sphere which is $V = \dfrac{4}{3}\pi {r^3}$
$\Rightarrow Q = \rho \times \dfrac{4}{3}\pi {r^3}$.
Now let us find the volume of the spherical ring which can be found out by subtracting the volume of sphere with radius $r$ with the sphere with radius $r + dr$
$\dfrac{4}{3}\pi {(r + dr)^3} - \dfrac{4}{3}\pi {r^3}$ [using the formula for ${(a + b)^3} = {a^3} + {b^3} + 3{a^2}b + 3a{b^2}$ and reducing the terms that would be too small to estimate] we get,
$\Rightarrow \dfrac{4}{3}\pi {r^3} + 4\pi {r^2}dr - \dfrac{4}{3}\pi {r^3} = 4\pi {r^2}dr$
Using the charge density of the sphere we can write $dQ = \rho .4\pi {r^2}dr$ . Now substitute the values of $Q$ and $dQ$ in the work done equation.
$\Rightarrow dU = \dfrac{{\rho .4\pi {r^2}dr \times \rho \times \dfrac{4}{3}\pi {r^3}}}{{4\pi {\varepsilon _0}r}}$ .
Simplifying the equation, we get, $dU = \dfrac{{4\pi {\rho ^2}{r^4}dr}}{{3{\varepsilon _0}}}$.
This is the work done to bring the charge from $r$ to $r + dr$ .To find the total energy needed to bring the charge from $r$ to $R$ will be,
$\int {dU = \int\limits_r^R {\dfrac{{4\pi {\rho ^2}{r^4}dr}}{{3{\varepsilon _0}}}} }$ [Integrating with respect to $r$ from $r = 0$ to $r = R$ ]
$\Rightarrow U = \dfrac{{4\pi {\rho ^2}{R^5}}}{{15{\varepsilon _0}}}$ is the electrostatic energy of a uniformly charged sphere of radius $R$
However integrating $\int {dQ} = \rho 4\pi \int\limits_0^R {{r^2}dr}$ with respect to $r$ with limits $r = 0$ and $r = R$ we get,
$Q = \dfrac{{\rho 4\pi {R^3}}}{3}$ . Rearranging and obtaining the value of $\rho$ we get $\rho = \dfrac{{3Q}}{{4\pi {R^3}}}$.
Substituting value of $\rho$ in the equation for electrostatic energy for an uniformly charged sphere of radius $R$ we get,
$U = \dfrac{{4\pi 9{Q^2}{R^5}}}{{16{\pi ^2}{R^6} \times 15{\varepsilon _0}}}$ . Simplifying the equation, we get,
$U = \dfrac{{3{Q^2}}}{{20\pi R{\varepsilon _0}}}$
Thus the electrostatic energy of an uniformly charged sphere of radius $R$ with total charge $Q$ is $U = \dfrac{{3{Q^2}}}{{20\pi R{\varepsilon _0}}}$.
Hence the correct answer is option C.

Note:
We could also possibly use the principle of superposition such that the sum of all the charges of the energy of a uniformly charged sphere are added, but it seems to be unlikely that is why we consider an imaginary element and carry out the task using it.