Question

A total charge $Q$ is broken into two parts ${{Q}_{1}}$ and ${{Q}_{2}}$ . They are placed at a distance $R$ from each other. The maximum force of repulsion will occur between them when-
(A). ${{Q}_{2}}=\dfrac{Q}{R}\,,\,{{Q}_{1}}=Q-\dfrac{Q}{R}$
(B). ${{Q}_{2}}=\dfrac{Q}{4}\,,\,{{Q}_{1}}=Q-\dfrac{2Q}{3}$
(C). ${{Q}_{2}}=\dfrac{Q}{4}\,,\,{{Q}_{1}}=\dfrac{3Q}{4}$
(D). ${{Q}_{1}}=\dfrac{Q}{2}\,,\,{{Q}_{2}}=\dfrac{Q}{2}$

Answer 1

As the charges are made of the same charge, they will carry the same type of charge on them, so a repulsive force exists between them. According to coulomb’s law, force is a function of charge. Therefore, using the force acting between them and differentiating it with respect to the variable charge, the values of ${{Q}_{1}}$ and ${{Q}_{2}}$ can be calculated.

Formula used:
$F=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\cdot \dfrac{{{Q}_{1}}{{Q}_{2}}}{{{r}^{2}}}$

Complete step by step solution:

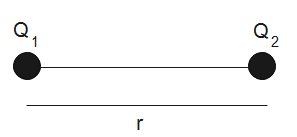
Force acting on a charge due to another charge is given by-
$F=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\cdot \dfrac{{{Q}_{1}}{{Q}_{2}}}{{{r}^{2}}}$ - (1)
${{\varepsilon }_{0}}$ is called the permittivity of free space
Given, the total charge is $Q$ . Let the charge on ${{Q}_{1}}$ be $Q'$ , then charge on ${{Q}_{2}}$ will be $Q-Q'$
Substituting these values in eq (1), we get,

& F=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\cdot \dfrac{Q'(Q-Q')}{{{r}^{2}}} \\\ & F=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\cdot \dfrac{Q'Q-Q{{'}^{2}}}{{{r}^{2}}} \\\ & \\\ \end{aligned}$$ As $$Q'$$ is variable, differentiating force with respect to $$Q'$$ , we get, $$\begin{aligned} & \dfrac{dF}{dQ'}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\cdot \dfrac{Q-2Q'}{{{r}^{2}}} \\\ & \text{when }\dfrac{dF}{dQ'}=0 \\\ & \dfrac{1}{4\pi {{\varepsilon }_{0}}}\cdot \dfrac{Q-2Q'}{{{r}^{2}}}=0 \\\ & \Rightarrow Q-2Q'=0 \\\ \end{aligned}$$ $$\therefore Q'=\dfrac{Q}{2}$$ The value of $$Q'$$ is $$\dfrac{Q}{2}$$ .Therefore, the value of $${{Q}_{1}}=\dfrac{Q}{2}$$ , the value of $${{Q}_{2}}$$ will be $$\begin{aligned} & {{Q}_{2}}=Q-Q'=Q-\dfrac{Q}{2} \\\ & {{Q}_{2}}=\dfrac{Q}{2} \\\ \end{aligned}$$ The values of $${{Q}_{1}}$$ and $${{Q}_{2}}$$ is $$\dfrac{Q}{2}$$ , therefore the correct option is (D). **So, the correct answer is “Option D”.** **Additional Information:** Electric field due to an electric charge is the force acting on a unit charge kept at a distance ( $$r$$ ) from it. Electric lines of forces are lines describing the electric field for an object, they are open lines and the direction of electric field is the same as the direction of electric lines of forces. **Note:** The forces acting on the charges due to each other are equal in magnitude but opposite in direction as it is a repulsive force. $$\varepsilon $$ is the permittivity of a medium , it tells us about the ability of a material to store potential difference under the influence of an electric field. The value of force changes with change in medium as the value of $$\varepsilon $$ is different for different mediums.