Question

A torch bulb rated $4.5W$, $1.5V$is connected to a battery with internal resistance of $2.67\Omega$ as shown in the figure. Find the EMF of the cell needed to make the bulb glow at full intensity.

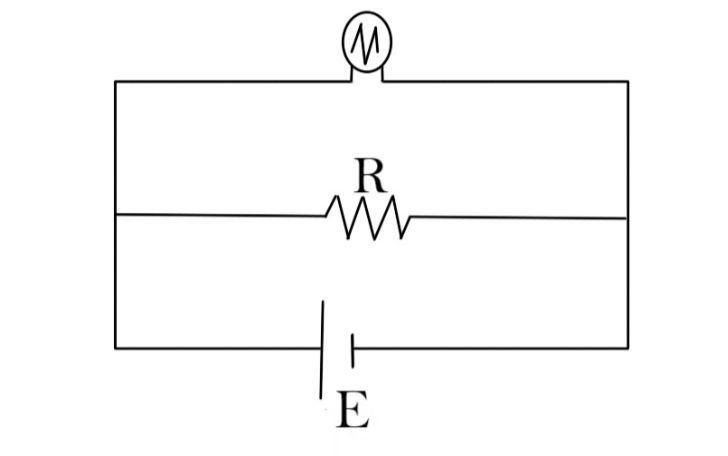
a. $4.5V$
b. $1.5V$
c. $2.67V$
d. $13.5V$

Answer 1

Hint: We have to find the total current and total resistance in the circuit. with this much information we can use Ohm’s law to find the emf.

Complete step by step answer:
Power of the bulb is given by
$P = \dfrac{{{V^2}}}{R}$

Where,
$V =$voltage of the bulb
$R =$resistance of the bulb

By using the formula we get,
$4.5W = \dfrac{{{{\left( {1.5V} \right)}^2}}}{R}$
$R = 0.5\Omega$

Two of the resistance are in parallel
Net resistance
$\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{0.5}} + \dfrac{1}{1}$
${R_{eq}} = 0.34\Omega$

The internal resistance of the battery is connected in series to ${R_{eq}}$.
Total resistance of the circuit $= 0.34\Omega + 2.67\Omega \\\ \approx 3\Omega \\\$

We know that,
$P = IV \\\ I = \dfrac{P}{V} \\\ I = \dfrac{{4.5}}{{1.5}} = 3A \\\$

Current is inversely proportional to resistance,
$I \propto \dfrac{1}{R}$
Let ${I_1}$ and ${I_2}$ be the current in $1\Omega$ resistance and bulb respectively.
So,
$\dfrac{{{I_1}}}{{{I_2}}} = \dfrac{{{R_2}}}{{{R_1}}}$
$\dfrac{{{I_1}}}{3} = \dfrac{1}{2}$
${I_1} = 1.5A$

Applying junction law at junction
Total current$= {I_1} + {I_2}$
Total current$= 3 + 1.5 = 4.5A$
Total resistance as calculated earlier$= 3\Omega$

By using OHM’S LAW
$E = IR \\\ E = 4.5A \times 3\Omega \\\ E = 13.5V \\\$

Therefore d) is the correct answer

Note: The voltage given in the question is the maximum voltage the bulb can bear. Therefore the resistance of the bulb is the maximum resistance it can offer in the circuit