Solveeit Logo
Login

Question

Question: \(A\to product\) and \(\left( \dfrac{dx}{dt} \right)=K{{[A]}^{2}}\). If log\(\left( \dfrac{dx}{dt} \...

A→productA\to product and (dxdt)=K[A]2\left( \dfrac{dx}{dt} \right)=K{{[A]}^{2}}. If log(dxdt)\left( \dfrac{dx}{dt} \right)is plotted against log [A], then graph is of the type:
A.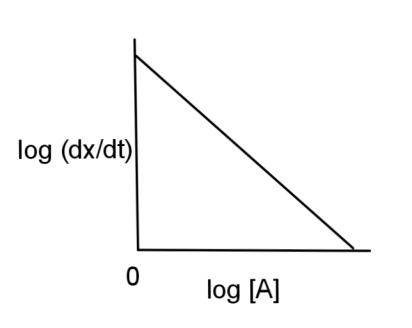
B.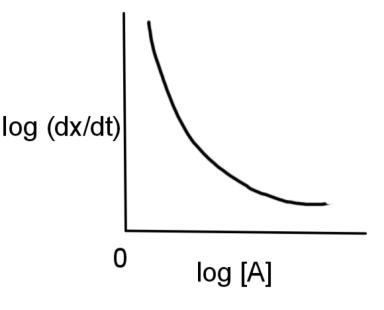
C.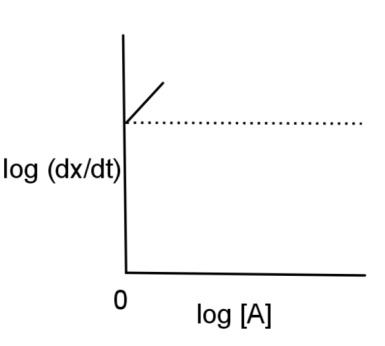
D.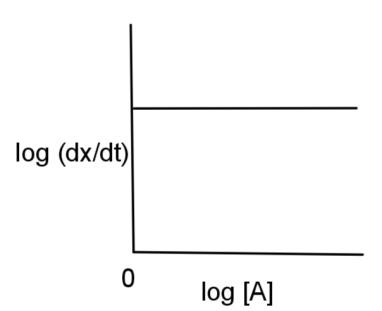

Explanation

Solution

Rate law is the concentration of the reactants that is raised to their stoichiometric coefficients. Here ‘K’ is the rate constant. While, (dxdt)\left( \dfrac{dx}{dt} \right) is the rate of a reaction in which the reactant is A. The graph of this expression can be identified by taking the log of the rate law, and then identifying the equation of slope, y = mx + c.

Complete answer:
The rate law of a reaction defines the rate of any reaction which is equal to the concentration of the species that are reacting and is raised to the power of their stoichiometric value. Rate constant of any reaction is the relationship between concentration of the reactants and the rate. The expression for which is rate=K[A]arate=K{{[A]}^{a}} where, ‘a’ is the stoichiometric coefficient and [A] is the concentration of reactant, and K is the rate constant.
We have been given graphs plotted between log forms of the integrated rate law. The integrated rate law is derived.
This is the second order reaction (involving one reactant A raised to power 2 as [A]2{{[A]}^{2}}), the equation will be 2A→products2A\to products. Applying the law of mass action, the rate of this reaction will be, dxdt∝[A]2\dfrac{dx}{dt}\propto {{[A]}^{2}}
So, changing the proportionality with rate constant k, we have,
dxdt=k[A]2\dfrac{dx}{dt}=k{{[A]}^{2}}, now, taking log on both the sides we have,
log⁡ (dxdt) =log⁡K+ 2log⁡[A]\log \,\left( \dfrac{dx}{dt} \right)\,=\log K+\,2\log [A]
Rearranging this equation, log⁡ (dxdt) = 2log⁡[A]+log⁡ K\log \,\left( \dfrac{dx}{dt} \right)\,=\,2\log [A]+\log \,K
The rearranged equation is similar to the equation of slope for a graph as y = mx + c, where,
m is the slope, x is the x coordinate, y is the y coordinate, and c is the intercept.
Therefore, the graph will have a straight line with slope as 2 and the intercept as log K and the graph will be

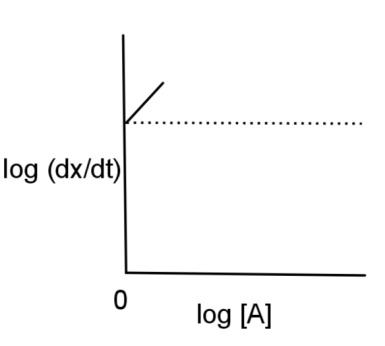
Hence, the log (dxdt)\left( \dfrac{dx}{dt} \right) is plotted against log [A] and has a graph of option C.

Note:
The tan of the angle of the slope will give us the value of 2. The value of log⁡ ab=b log⁡ a\log \,{{a}^{b}}=b\,\log \,a, is used in the log form of the equation, also the relation, log (ab) = log a + log b is used to derive the equation of slope in the log form. The slope- intercept form of the equation can tell us the value of rate constant, which is the slope of the graph between concentration and time.