Question

A time varying magnetic field, $(\vec B = {B_0}t\hat k)$ , is confined in a cylindrical region and is cutting the XY plane on a circle ${x^2} + {y^2} = 4$ where $x$ and $y$ are in meters. A wire frame ${A_1}{A_2}{A_4}{A_3}{A_1}$ is placed in the magnetic field as shown. Segments ${A_1}{A_2}$ and ${A_3}{A_4}$ are identical quarter circles parallel to each other with axes along the $Z$ -axis. The induced current flowing in the wire frame is equal to: (The total length of the loop of wire frame is $10m$ , the radius of arc ${A_1}{A_2}$ and arc ${A_3}{A_4}$ is $1m$ each and resistance per unit length is $1\Omega {m^{ - 1}}$ ):

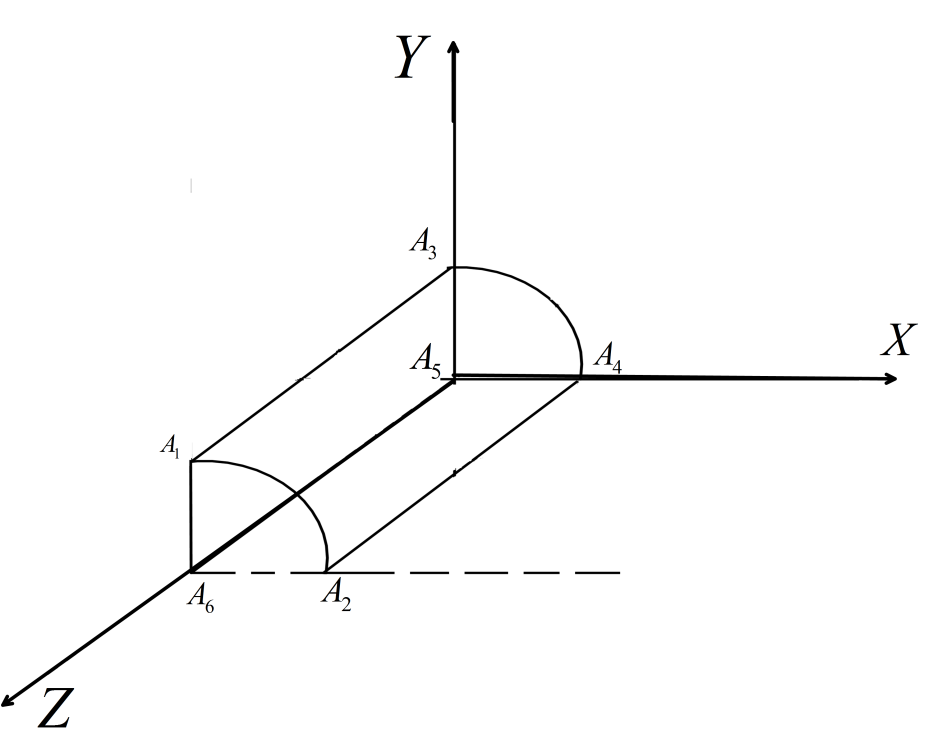
(A) zero
(B) $\dfrac{{{B_0}\pi }}{{10}}$
(C) $\dfrac{{{B_0}\pi }}{5}$
(D) $\dfrac{{{B_0}\pi }}{{20}}$

Answer 1

Hint : From Lenz’s laws we know that change of magnetic field with time induce a voltage across a current loop kept in the magnetic field. The induced E.M.F across the loop is given by, $\xi = - \dfrac{{d\varphi }}{{dt}}$ .

Complete Step By Step Answer:
We know that Lenz's law states that the current induced in a circuit due to a change in a magnetic field is directed to oppose the change in flux and to exert a mechanical force which opposes the motion. The magnitude of E.M.F induced in a coil is proportional to the rate of change of the magnetic field. The expression is given by, $\xi = - \dfrac{{d\varphi }}{{dt}}$ .
Now, we know that magnetic flux induced in a closed surface is given by, $\varphi = \oint {\vec B \cdot d\vec S}$ where, $\vec B$ is the magnetic field of the region.

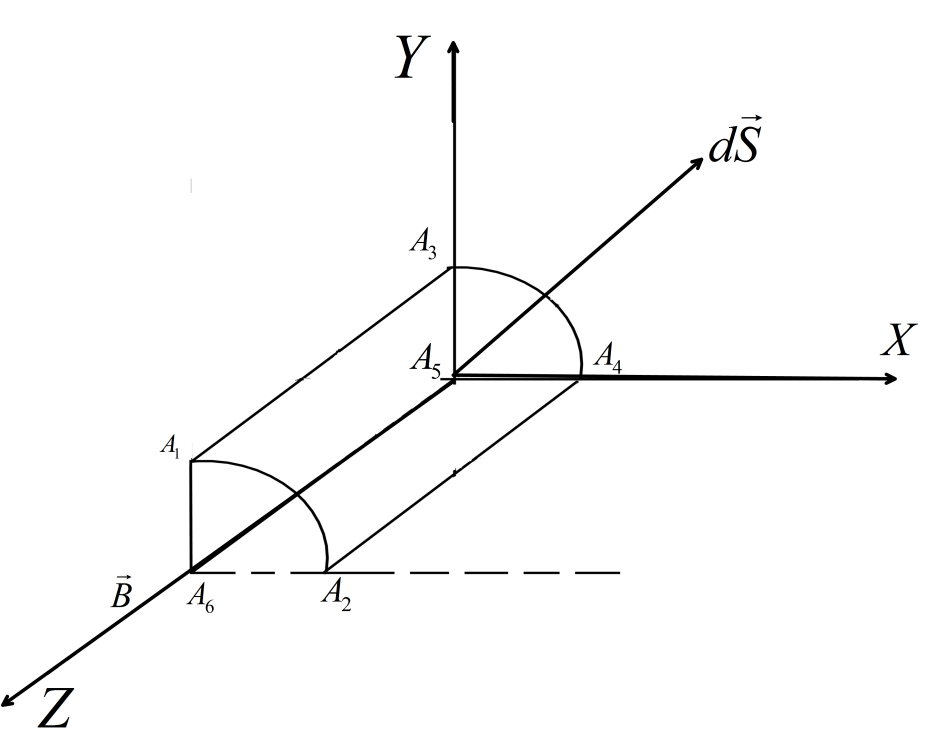
Here, we can see that the magnetic field is along the axis of the cylindrical surface that means the surface vector is always radially outward. So, it is certain that the surface is perpendicular to the magnetic field . Hence, there is no component of the magnetic field along the surface. So, Net flux through the wire frame ${A_1}{A_2}{A_4}{A_3}{A_1}$ must be zero. So, we can write, $\varphi = \oint {\vec B \cdot d\vec S} = 0$ .

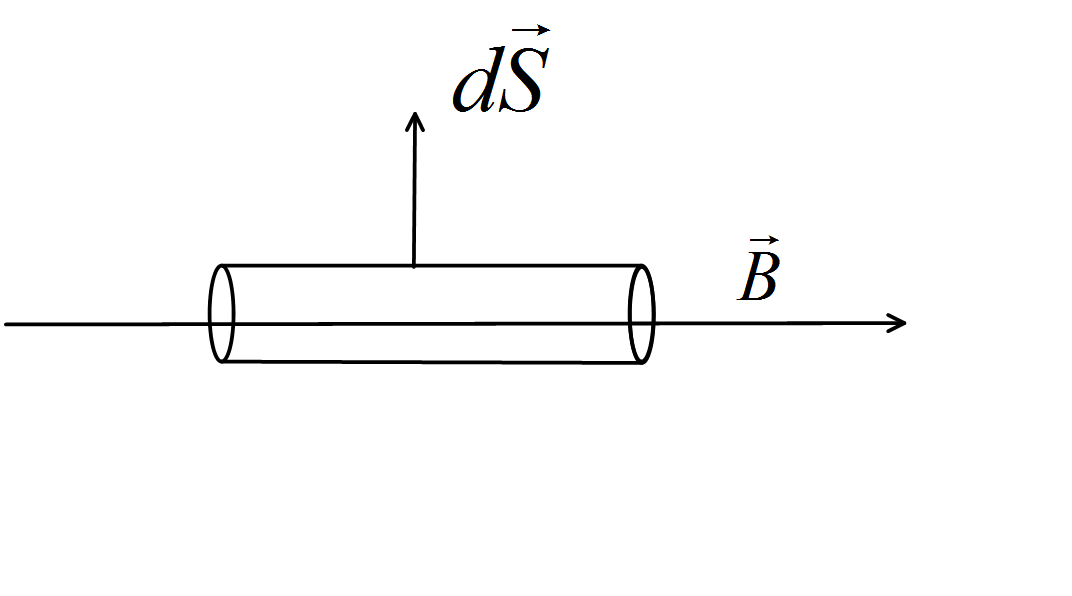
So, the induced voltage across the frame also be zero , i.e. $\xi = - \dfrac{{d\varphi }}{{dt}} = 0$
Now, from Ohm’s law we know, current, $I = \dfrac{V}{R}$ .
So, putting the value of induced E.M.F in the Ohm’s law we get, current, $I = \dfrac{\xi }{R} = 0$ .
So, the current through the frame ${A_1}{A_2}{A_4}{A_3}{A_1}$ will be zero.

Note :
$\bullet$ If the magnetic field vector has a component along X axis or Y axis then the flux through the frame is non zero, then there is a finite current through the frame.
$\bullet$ For a uniform magnetic field the induced E.M.F across the frame will always be zero.