Question

A tightly wound long solenoid has n turns per unit length, radius r, and carries a current i. A particle having charge q and mass m is projected from a point on the axis in the direction perpendicular to the axis. The maximum speed for which the particle doesn’t strike the solenoid will be –

& \text{A) }\dfrac{{{\mu }_{0}}qrni}{2m} \\\ & \text{B) }\dfrac{{{\mu }_{0}}qrni}{m} \\\ & \text{C) }\dfrac{2{{\mu }_{0}}qrni}{3m} \\\ & \text{D) None of these} \\\ \end{aligned}$$

Answer 1

We are given that a charged particle is released from an axis inside a solenoid. We can use the equation for magnetic Lorentz force and the centripetal force to determine the maximum radius at which the particle can undergo circular motion.

Complete step by step answer:
It is given to us that a solenoid is wound tightly about an axis which passes through the point O as shown below. Also, we know that charged particles are released from this axis perpendicular to it such that the particle can undergo circular motion within the solenoid.

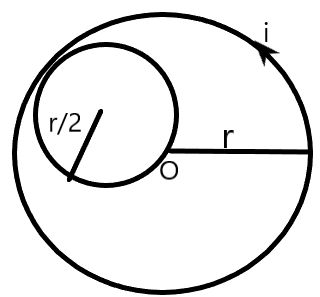
We know that a charged particle projected perpendicular to a magnetic field will undergo circular motion. So, the given particle projected inside the solenoid also undergoes a circular motion.
It is given that the radius of the solenoid is ‘r’. For the charged particle not to strike the solenoid, the maximum radius in which it can undergo circular motion will be half the radius of the solenoid as shown in the figure.
We can find this radius by equating the Lorentz force and the centripetal force on the charged particle. Which is given as –

& {{\text{F}}_{B}}=qvB\sin \theta \\\ & \text{but, here }\theta \text{=9}{{\text{0}}^{0}} \\\ & \therefore {{F}_{B}}=qvB \\\ & \text{and,} \\\ & {{F}_{c}}=\dfrac{m{{v}^{2}}}{r} \\\ \end{aligned}$$ For the particle to undergo circular motion these two forces should be equal. $$\begin{aligned} & {{F}_{B}}={{F}_{c}} \\\ & \Rightarrow qvB=\dfrac{m{{v}^{2}}}{\dfrac{r}{2}} \\\ & \Rightarrow v=\dfrac{qrB}{2m} \\\ \end{aligned}$$ But we also know the magnetic field due to a solenoid we ‘n’ turns per unit length as – $$B={{\mu }_{0}}ni$$ Substituting this in the equation for velocity gives – $$\therefore v=\dfrac{q{{\mu }_{0}}nir}{2m}$$ The velocity at which the particle moves should be less than or equal to $$\dfrac{{{\mu }_{0}}qnir}{2m}$$. **The correct answer is option A.** **Note:** A charge particle in a magnetic field will undergo a circular motion if it has a perpendicular component along the direction of the magnetic field. The Lorentz force acting on the particle will be zero if the particle was moving along the axis and hence no circular motion.