Question

(a) Three resistors of resistances $2\Omega$, $3\Omega$ and $4\Omega$ are combined in series. What is the total resistance of the combination?
(b) If this combination is connected to a battery of emf $10V$ and negligible internal resistance, find the potential drop across each resistor.

Answer 1

A complex circuit with two or more resistors connected to each other can be easily reducing the circuit into a much simpler form. The resistances in series formula is applied in order to determine the total resistance of the circuit in series combination. The potential drop of each resistor will be different due to the difference in resistor values and the ohm’s law formula is applied in order to find the voltage values.

Complete step by step answer:
The problem revolves around the concept of resistances in series combination and the ohm’s law concept. In order to find the total resistance of the circuit and the respective potential drops we first need to understand the concept of ohm’s law and the equation governing the resistors in series.

(a) A series combination, as the name implies, is said to be a circuit in which a number of resistors are connected end to end so that they are all connected by a single wire in which all the resistors are attached in series to each other. In a combination of two or more resistances which are connected in series or parallel, there is a method wherein they are replaced by a single resistance value and this process is known as reducing of the circuit.

The total resistance used to replace the complex circuit of resistors by a single resistance value is called the equivalent resistance whose value is what we are required to find.The below diagram illustrates how the resistances are connected in series:

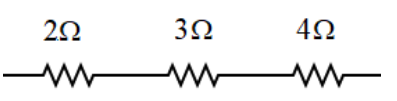
An equation to find the equivalent resistance is given in accordance to the concept of resistances connected in series. The resistances in series equation states that if a number of resistances are connected in series then their equivalent that is the net resistance will be the sum of the individual resistances.
This is given by the equation:
${R_s} = {R_1} + {R_2} + {R_3} + .... + {R_n}$ ------($1$)
Where, $n$ is any positive integer.

We are given that the combination includes three resistors that are connected in series to each other. Hence, the value of $n$ becomes $3$.
Since, $n = 3$, equation ($1$) becomes:
${R_s} = {R_1} + {R_2} + {R_3}$ ---------($2$)
We are given these values of resistors to be $2\Omega$, $3\Omega$ and $4\Omega$ respectively. These values are then substituted in equation ($2$). Hence the equivalent resistance, that is, the total resistance of this series combination will be:
${R_{eq}} = 2 + 3 + 4$
By solving out the equation we get the equivalence resistance to be:
${R_{eq}} = 9\Omega$
Thus, this is the total resistance of the series combination.

(b) We now apply the ohm’s law which gives the relationship between current and voltage, that is, the potential drop across the resistor. The ohm’s law equation is given by the equation:
$V = I{R_{eq}}$ --------($3$)
In a series combination, the same amount of current flows through each one of the resistors connected in series while the potential difference across the entire circuit will be equal to the sum of potential drops across each resistor in series.

This is because the current flows through a single conductor wire without having to split up in any junction. However, the potential drop occurs due to the resistance offered by a resistor. This potential drop is measured across the ends of each resistor. The circuit is given below:

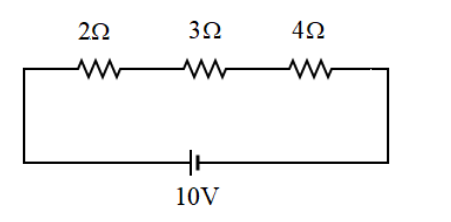
Each resistor will be having its own potential drop across it which we are asked to find. To find this we first need to find out the current across the circuit will be the same across all the resistors. We are already given the voltage to be $10V$ and let us consider the equivalent resistance that we calculated in part a) since current is constant. Thus we substitute this in equation ($3$) to get:
$10 = I\left( 9 \right)$

We rearrange the terms to find the current value:
$I = \dfrac{{10}}{9}$
$\Rightarrow I \approx 1.11A$
Hence this is the total current of the circuit.
For the $2\Omega$ resistor we apply the ohm’s law equation again:
$V = \left( {1.11} \right)\left( 2 \right)$
$\Rightarrow V = 2.22V$
Hence, this is the potential drop across the $2\Omega$ resistor.
For the $3\Omega$ resistor we apply the ohm’s law equation again:
$V = \left( {1.11} \right)\left( 3 \right)$
$\Rightarrow V = 3.33V$
Hence, this is the potential drop across the $3\Omega$ resistor.
For the $4\Omega$ resistor we apply the ohm’s law equation again:
$V = \left( {1.11} \right)\left( 3 \right)$
$\therefore V = 4.44\,V$
Hence, this is the potential drop across the $4\Omega$ resistor.

Note: The equivalent resistance is what is supposed to be used in the ohm’s law equation to find out the potential drops across each resistor but the resistance of the resistor across which voltage is to be measured is substituted instead which is incorrect. This is a common error which is made in these types of problems. Equivalence resistance is usually larger than the largest individual resistance in the case of series combination.