Question

A thin wire of length l and mass M is bent in the form of a semicircle. What is its moment of inertia about an axis passing through the ends of the wire?

Answer 1

Begin by taking an elementary mass over the circumference of the semi-circle spanning an elementary angle of $\theta$. Then, obtain an expression for the elementary moment of inertia MI and integrate this over the entire angular span (0 to $\pi$) of the semi-circle. Remember to consider the linear distance between the axis of rotation and the elementary mass while taking the distance of the elementary mass. This will be an angular component of the radius of the semi-circle. Once you have obtained the expression for MI, substitute r in terms of l given that the length of the wire forms the circumference, and to this end, arrive at the appropriate result.

Formula used: Moment of inertia for a half-ring: $I = \dfrac{Mr^2}{2}$

Complete step by step answer:
Since the thin wire is bent into a semi-circle, the length of the wire becomes the circumference of the semi-circle, i.e.,
$l = \pi r \Rightarrow r = \dfrac{l}{\pi}$
The moment of inertia of the semicircle about the axis YY’ can be derived by first taking an elementary mass dm over the circumference of the semi-circle, and integrating the elementary moment of inertia over the entire circumference to obtain the total inertia.
$I = \int dI = \int dm\;r^{\prime^2}$, where $r^{\prime} = r cos\theta$ is the linear distance to the circumference from the axis of rotation YY’.

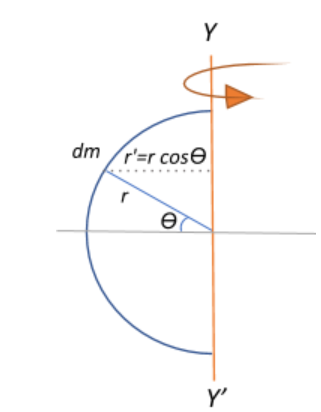
We know that the elementary mass is an angular unit of the entire mass of the semi-circle ${dm} = \dfrac{M}{\pi}d\theta$, where $\pi$ is the angular span of the semi-circle.
$\Rightarrow I = \int \dfrac{M}{\pi}d\theta. r^2cos^2\theta = \dfrac{Mr^2}{\pi} {}\int_0^{\pi}cos^2\theta d\theta$
$\Rightarrow I = \dfrac{Mr^2}{\pi}\left|\dfrac{1}{2}\theta + \dfrac{sin2\theta}{4} \right|_{0}^{\pi}$
$\Rightarrow I = \dfrac{Mr^2}{\pi}\left(\dfrac{\pi}{2} + 0\right)$
$\Rightarrow I = \dfrac{Mr^2}{2}$
Now, given that $r = \dfrac{l}{\pi}$
$I = \dfrac{1}{2}M\left(\dfrac{l}{\pi}\right)^2 = \dfrac{Ml^2}{2\pi^2}$

Note: To explain the integral of $cos^2\theta\;d\theta$:
$\int cos^2\theta\;d\theta = \int \dfrac{1+cos2\theta}{2}d\theta = \int \dfrac{1}{2}d\theta + \dfrac{1}{2}\int cos2\theta\;d\theta$
$\Rightarrow \int cos^2\theta\;d\theta = \dfrac{1}{2}\theta + \dfrac{1}{2}\times \dfrac{sin2\theta}{2} = \dfrac{\theta}{2}+\dfrac{sin2\theta}{4}$
Also, remember that the moment of inertia is dependent on the distribution of mass of the system about the axis of rotation, the position and orientation of the axis of rotation and the shape of the body constituting the system.