Question

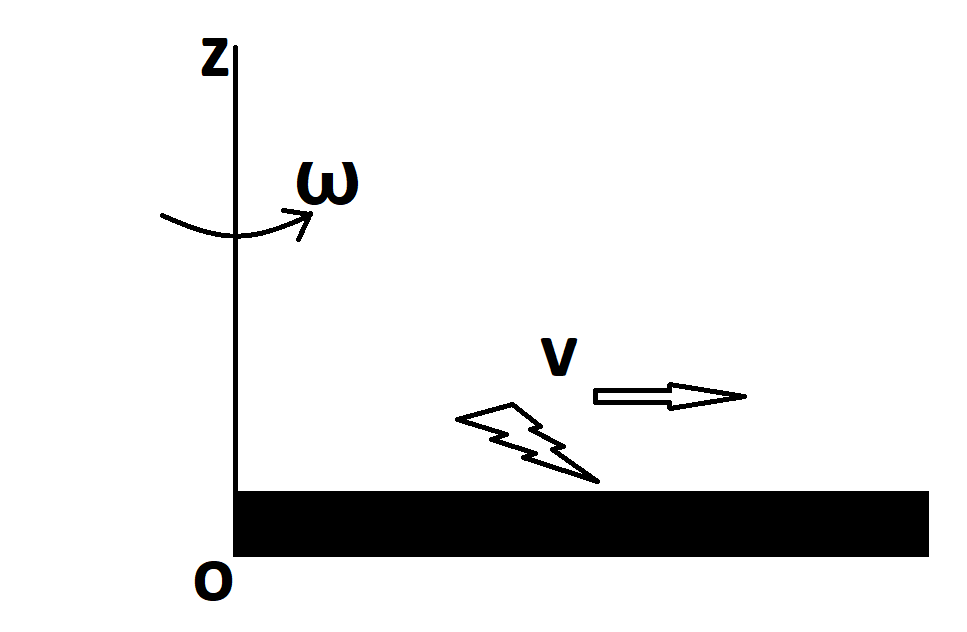
A thin uniform rod, pivoted at O, is rotating in the horizontal plane with constant angular speed $\omega$ , as shown in the figure. At time t = 0, a small insect starts from O and moves with constant speed v, with respect to the rod towards the other end. It reaches the end of the rod at t =T and stops. The angular speed of the system remains $\omega$ throughout. The magnitude of the torque $\left( \left| {\vec{\pi }} \right| \right)$ about O, as a function of time is best represented by which plot?

A.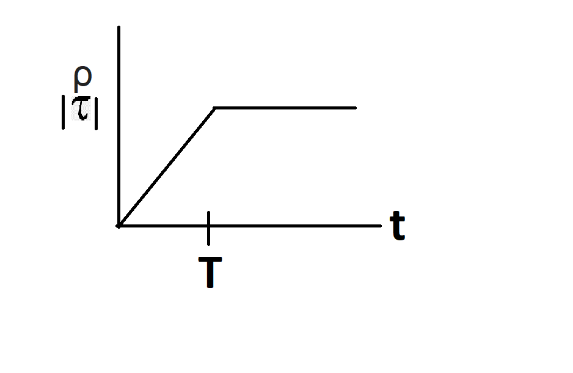
B.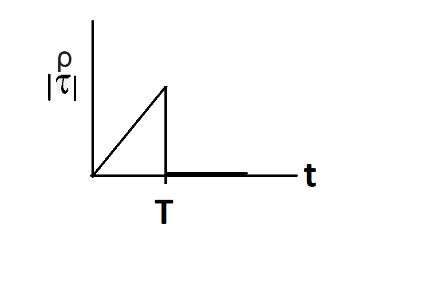
C.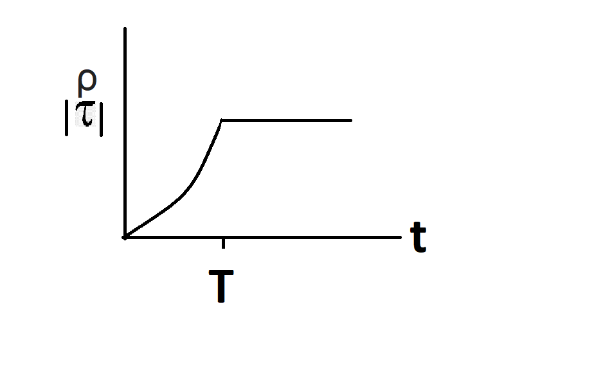

D.

Answer 1

This question is a case of hinged rotational motion. To get the correct answer you have to find out the relationship between $\tau$and time. For that you can proceed by using the formula for $\tau$ and moment of inertia. Remember that $|\vec{r}|=|\dfrac{d\vec{L}}{dt}|$. Also, remember the moment of inertia will be that of rod, i.e., $\dfrac{1}{3}M{{L}^{2}}$ plus that of the $m{{x}^{2}}$ for the object where x is an arbitrary distance.

Complete answer:
As we know,
$|\vec{r}|=|\dfrac{d\vec{L}}{dt}|$
Where
$L=I\omega$
So,
Now,
It is obvious from the scenario that the moment of inertia is
The (rod + insect) scheme is increasing.

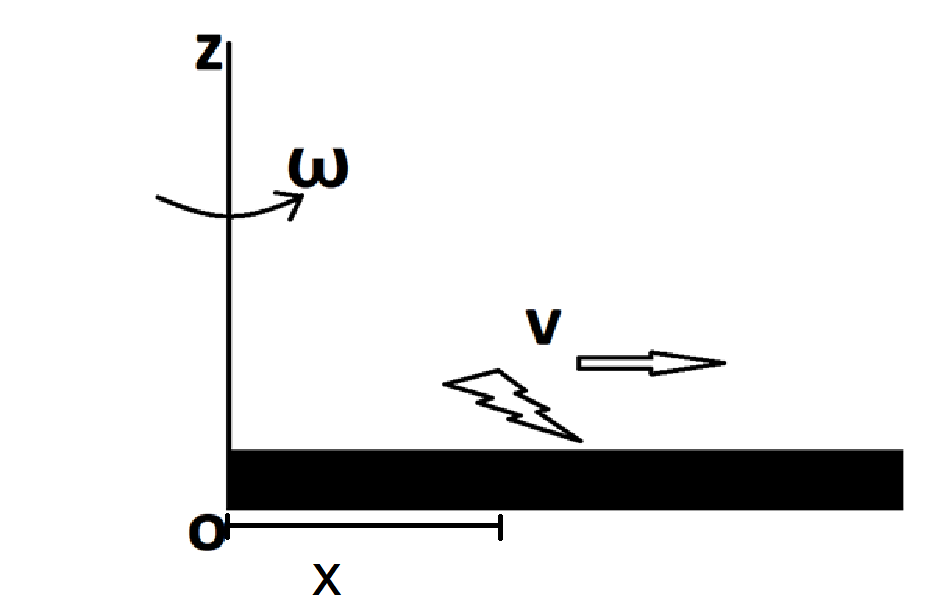
Let the insect be at a distance xx at any moment in time,' t'
Of O. At this time, the time of the inertia of the moment,
The scheme is
So,
Then
$\tau =\dfrac{d}{dt}(I\omega )=\omega \dfrac{dl}{dt}$
Therefore,
$I=\dfrac{1}{3}M{{L}^{2}}+m{{x}^{2}}............$ ……………. (ii)
Now,
By using the equations (i) and (ii)
We have
$\tau =\omega \dfrac{d}{dt}[\dfrac{1}{3}M{{L}^{2}}+m{{x}^{2}}]$
$\Rightarrow \tau =\omega m\dfrac{d}{dt}{{x}^{2}}$
$\Rightarrow \tau =\omega m2x\dfrac{dx}{dt}$
$\Rightarrow \tau =2\omega mxu$
$\Rightarrow \tau =2\omega m{{v}^{2}}t$
So,
Form the above equation, we can easily conclude that
$\tau \propto t$
At t=T, υ=0.
Therefore, $\tau =0$
Hence, the graph between $\tau$ and tis a straight line till t=T. Also, for, t>T, $\tau =0$
Option - B is the correct option.

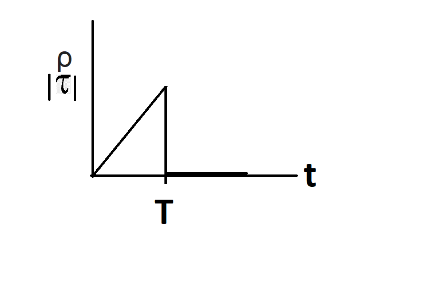
Note:
As you can see, the final result was $\tau \propto t$ that can be written as $\tau =kt$where k is some constant. So, the graph will be that of a straight line. While in exam, you can sometimes save your time by eliminating the options which have any curve other than the straight line.