Question

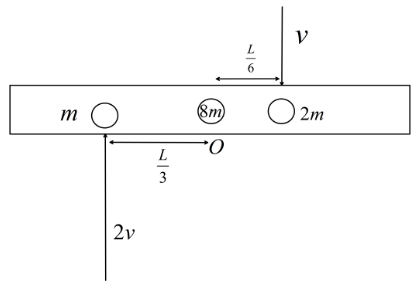
A thin uniform bar of length $L$ and mass $8m$ lies on a smooth horizontal table. Two point masses $m$ and $2m$ moving in the same horizontal plane from opposite sides of the bar with speeds $2v$ and $v$ respectively. The masses stick to the bar after collision at a distance $\dfrac{L}{3}$ and $\dfrac{L}{6}$ respectively from the centre of the bar. If the bar starts rotating about its center of mass as a result of collision, the angular speed of the bar will be:

A. $\dfrac{v}{{5L}}$
B. $\dfrac{{6v}}{{5L}}$
C. $\dfrac{{3v}}{{5L}}$
D. $\dfrac{v}{{6L}}$

Answer 1

Use conservation of angular momentum to find the angular velocity of the whole system. The conservation of angular momentum states that the angular momentum of a system is conserved when net applied torque is zero.

Formula used: Conservation of angular momentum is given by,
${L_i} = {L_f}$
where, ${L_i}$ is the initial angular momentum and ${L_f}$ iis the final angular momentum of the system.
Centre of mass of a body is given by,
$R = \dfrac{{\sum {{m_i}{r_i}} }}{{\sum {{m_i}} }}$
where $R$ is the centre of mass about the origin${m_i}$ is the mass of the $ith$ particle ${r_i}$ is the position vector about the origin of the $ith$ particle.
Angular momentum of a body about a point is given by,
$L = mvr = I\omega$
where, $m$ is the mass of the particle, $v$ is the velocity of the particle and $r$ is the distance from the axis, $I$ is the moment of inertia about the axis and $\omega$ is the angular velocity.
The moment of inertia of a rod of length $L$ is,
$I = \dfrac{{M{L^2}}}{{12}}$
where, $M$ is the mass of the rod.
Moment of inertia of any body of $m$ about the centre of mass is given by,
$I = m{r^2}$ where $r$ is the distance from the centre of mass.

Complete step by step answer:
Here, the two masses collide with the rod and are stuck together, so the masses become the part of the system hence the external torque applied must be zero. So, angular momentum of the system must be conserved. We know that centre of mass of a body is given by,
$R = \dfrac{{\sum {{m_i}{r_i}} }}{{\sum {{m_i}} }}$
Now, the centre of mass of the system after collision about the point $O$ will be,
$R = \dfrac{{8m(0) + 2m(\dfrac{L}{6}) - m\dfrac{L}{3}}}{{8m + 2m + m}}$
$\Rightarrow R = 0$
So, after collision the centre of mass of the system will be also at point O.
We also know, angular momentum of a body about a point is given by,
$L = mvr = I\omega$
Now, angular momentum of the system before collision about O is,
${L_i} = m(2v)\dfrac{L}{3} + 2m(v)\dfrac{L}{6}$.
$\Rightarrow {L_i} = \dfrac{{2mvL}}{3} + \dfrac{{mvL}}{3}$
Hence we have, ${L_i} = mvL$

Now, let’s say the angular speed after collision of the system is, $\omega$
So, angular momentum of the system after collision about $O$ is,
${L_f} = ({I_{rod}} + {I_m} + {I_{2m}})\omega$
Now, moment of inertia of a rod about centre of mass is given by,
$I = \dfrac{{M{L^2}}}{{12}}$
So, here, ${I_{rod}} = \dfrac{{8m{L^2}}}{{12}}$
Moment of inertia of the mass $m$ is, ${I_m} = m{\left( {\dfrac{L}{3}} \right)^2} = \dfrac{{m{L^2}}}{9}$
Moment of inertia of the mass $2m$ is, ${I_{2m}} = 2m{\left( {\dfrac{L}{6}} \right)^2} = \dfrac{{m{L^2}}}{{18}}$

So, we get, ${L_f} = ({I_{rod}} + {I_m} + {I_{2m}})\omega$
${L_f} = (\dfrac{{8m{L^2}}}{{12}} + \dfrac{{m{L^2}}}{9} + \dfrac{{m{L^2}}}{{18}})\omega$
$\Rightarrow {L_f} = m{L^2}(\dfrac{8}{{12}} + \dfrac{1}{9} + \dfrac{1}{{18}})\omega$
$\Rightarrow {L_f} = m{L^2}(\dfrac{2}{3} + \dfrac{1}{9} + \dfrac{1}{{18}})\omega$
So, simplifying we have,
${L_f} = \dfrac{5}{6}m{L^2}\omega$.
Hence, we can write, ${L_i} = {L_f}$
So, equating the values we have,
$mvL = \dfrac{5}{6}m{L^2}\omega$
Up on simplifying we have,
$\therefore \omega = \dfrac{{6v}}{{5L}}$.
Hence, the system will rotate with an angular speed of $\dfrac{{6v}}{{5L}}$.

Hence, option B is correct.

Note: Always remember that if after collision both the masses travel apart and do not stick with the rod then the net torque will not be zero. If the centre of mass of the system gets shifted we have to calculate the moment of inertia about that point for each object. Then the moment of inertia of the rod will not be equal to $\dfrac{{M{L^2}}}{{12}}$. But, we can use parallel axis theorem to find the moment of inertia of the rod about the new centre of mass then. Also, the length between the masses and the new centre of mass will be different then also we have to calculate the changed distance from the centre of mass by subtracting or adding length.