Question

A thin, symmetric double convex lens of power $P$ is cut into $3$ parts $A$, $B$ and $C$ as shown. The power of

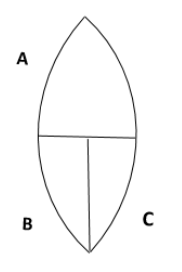
$A)$ $A$ is $P$
$B)$ $A$ is $2P$
$C)$ $B$ is $\dfrac{P}{2}$
$D)$ $C$ is $\dfrac{P}{4}$

Answer 1

Here, we are considering the relation between power and focal length and how the cutting affects the focal length of the lens. The change in power will only occur if there will be any change in focal length. We also need a relation between the radius of curvature and focal length of a lens (lens maker’s equation).
Formula Used:
$f=\dfrac{1}{P}$
$\dfrac{1}{f}=\left( {{\mu }_{2}}-1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)$

Complete answer:
When we examine the given figure and see how the lens is cut into $3$ parts, we can understand that there is no change in the radius of curvatures of part $A$. That means there will be no change in the focal length of part $A$.

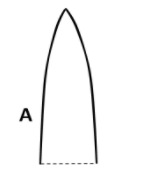
As there is no change in the focal length of part $A$, there will be no change in power also.
That is, the power of part $A$ remains the same, which is $P$ itself. So, option A is correct.
Now, if we examine part $B$,

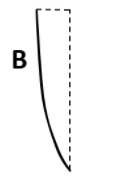
Here, the radius of curvature on one side remains the same but the other side becomes plane. So this will affect the focal length. The new focal length can be found using the lens makers formula and rearranging it for each case.
$\dfrac{1}{f}=\left( {{\mu }_{2}}-1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)$
$\Rightarrow \dfrac{{{f}_{old}}}{{{f}_{new}}}=\dfrac{\left( \dfrac{1}{{{R}_{{}}}}-\dfrac{1}{-{{R}_{{}}}} \right)}{\left( \dfrac{1}{{{R}_{old}}}-\dfrac{1}{0} \right)}=\dfrac{\dfrac{2}{R}}{\dfrac{1}{R}}=2$
Therefore, ${{f}_{new}}=2{{f}_{old}}$. That means focal length is doubled.
Then, the change in power of part $B$ will be,

& P=\dfrac{1}{f} \\\ & \Rightarrow \dfrac{{{P}_{old}}}{{{P}_{new}}}=\dfrac{{{f}_{new}}}{{{f}_{old}}} \\\ & \Rightarrow \dfrac{{{P}_{old}}}{{{P}_{new}}}=\dfrac{2{{f}_{old}}}{{{f}_{old}}} \\\ & \Rightarrow {{P}_{new}}=\dfrac{{{P}_{old}}}{2} \\\ \end{aligned}$$ Therefore, the power of part $$B$$ be halved. i.e., $$\dfrac{P}{2}$$. So, option c is also correct. Now, if we take part $$C$$, it will be the same as part $$B$$ but carries a negative charge because unlike $$B$$ the first surface is plain and second is having curvature. The resulting focal length will be $$-2f$$ and power will be $$\dfrac{-P}{2}$$. **Altogether, this question has 2 right answers which are option a and option c.** This is because part $$A$$ retains its power and part $$B$$ will be having half the power of the original lens as an effect of cutting. **Note:** While doing this problem, we must be aware of the changes happening to the parts that the lens is cut into. When we are substituting the changed radius of curvature, try to know which surface has changed. This question will seem easier if we can just understand the change in focal length by looking at the figure.