Solveeit Logo
Login

Question

Question: A thin spherical insulating shell of radius \( R \) carries a uniformly distributed charge such that...

A thin spherical insulating shell of radius RR carries a uniformly distributed charge such that the potential at its surface is V0{{V}_{0}} ​. A hole with a small area α4πR2(α⟨⟨1)\alpha 4\pi {{R}^{2}}\left( \alpha \langle \langle 1 \right) is made on the shell without affecting the rest of the shell. Which one of the following statements is found to be correct?
A. the ratio of the potential at the centre of the shell to that of the point at 12R\dfrac{1}{2}R from centre towards the hole will be 1−α1−2α\dfrac{1-\alpha }{1-2\alpha }
B. the potential at the centre of shell is reduced by 2αV02\alpha {{V}_{0}}
C. the magnitude of electric field at the centre of the shell is reduced by αV02R\dfrac{\alpha {{V}_{0}}}{2R}
D. the magnitude of electric field at a point, located on a line passing through a hole and shell’s centre, on a distance 2R2R from the centre of the spherical shell will be reduced by αV02R\dfrac{\alpha {{V}_{0}}}{2R}

Explanation

Solution

Gauss’s law can be helpful in solving this question. Gauss's law is also called Gauss's flux theorem. This law is related to distribution of electric charge to the net electric field. The surface under consideration should be a closed one which is having a volume like a spherical surface.

Complete step-by-step answer:

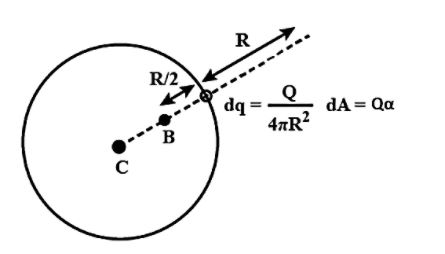
We know that the potential at a surface is given as,
V0=KQR{{V}_{0}}=\dfrac{KQ}{R} EC=KαQR2=αV0R{{E}_{C}}=\dfrac{K\alpha Q}{{{R}^{2}}}=\dfrac{\alpha {{V}_{0}}}{R}
And also the potential at the centre C will be,
VC=KQR−KαQR=V0(1−α){{V}_{C}}=\dfrac{KQ}{R}-\dfrac{K\alpha Q}{R}={{V}_{0}}\left( 1-\alpha \right)
Potential at the point B will be,
VB=KQR−KαQR2=V0(1−2α){{V}_{B}}=\dfrac{KQ}{R}-\dfrac{K\alpha Q}{\dfrac{R}{2}}={{V}_{0}}\left( 1-2\alpha \right)
Taking the ratio between these two can be written as,
VcVB=(1−α)(1−2α)\dfrac{{{V}_{c}}}{{{V}_{B}}}=\dfrac{\left( 1-\alpha \right)}{\left( 1-2\alpha \right)}
The electric field acting at the point A is,
EA=KQ(2R)2−KαQR2=KQ4R2−αV0R{{E}_{A}}=\dfrac{KQ}{{{\left( 2R \right)}^{2}}}-\dfrac{K\alpha Q}{{{R}^{2}}}=\dfrac{KQ}{4{{R}^{2}}}-\dfrac{\alpha {{V}_{0}}}{R}
That is the electric field will be reduced byαV0R\dfrac{\alpha {{V}_{0}}}{R},
The electric field experienced at C is given as,
EC=KαQR2=αV0R{{E}_{C}}=\dfrac{K\alpha Q}{{{R}^{2}}}=\dfrac{\alpha {{V}_{0}}}{R}
That is, the electric field at C is increasing byαV0R\dfrac{\alpha {{V}_{0}}}{R}.

So, the correct answer is “Option A”.

Note: Electric field is described as the electric force experiencing per unit charge. The direction of the field is the same as the direction of the force it would exert on a positive test charge. The electric field is radially outward in the case of a positive charge and radially inwards for a negative point charge.