Solveeit Logo
Login

Question

Question: A thin slab of thickness t with variable refractive index. The index vary with h (distance from prin...

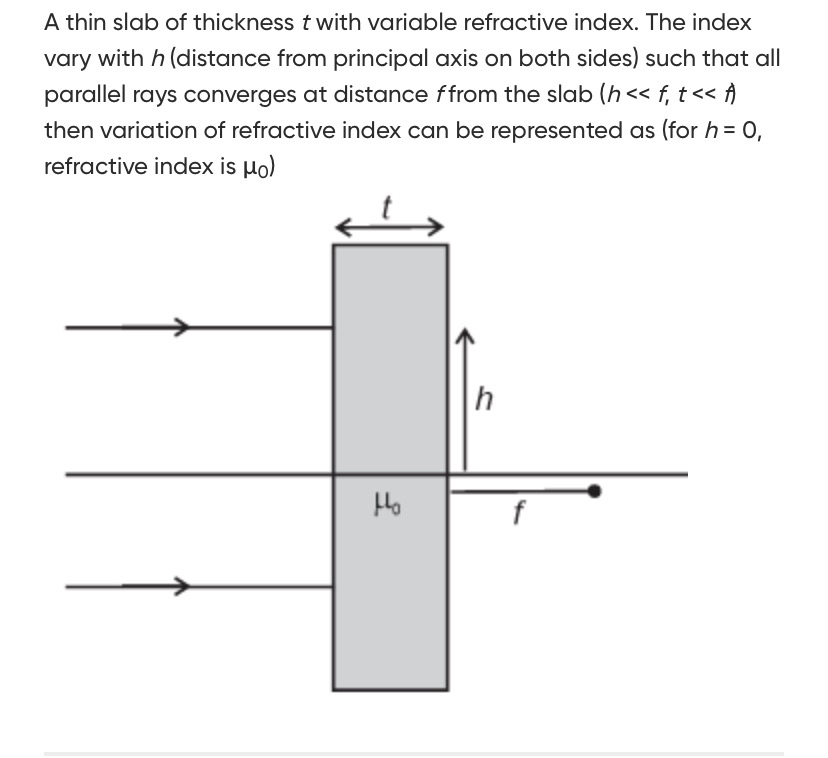
A thin slab of thickness t with variable refractive index. The index vary with h (distance from principal axis on both sides) such that all parallel rays converges at distance f from the slab (h << f, t << f) then variation of refractive index can be represented as (for h = 0, refractive index is μ0\mu_0)

Answer

μ(h)=μ0−h22tf\mu(h) = \mu_0 - \frac{h^2}{2tf}

Explanation

Solution

The problem describes a thin slab with a variable refractive index μ(h)\mu(h), where hh is the distance from the principal axis. Parallel rays incident on this slab converge at a distance ff from the slab. We are given that h≪fh \ll f and t≪ft \ll f, which allows us to use paraxial approximations. The refractive index at h=0h=0 is μ0\mu_0.

According to Fermat's principle, for all rays originating from a point (or from a plane wavefront, effectively from infinity for parallel rays) and converging to another point, the optical path length (OPL) must be constant.

Let's consider an incident plane wavefront at the left surface of the slab (say, at x=0x=0). The rays are parallel to the principal axis (x-axis). The focal point is F(f,0)F(f, 0).

  1. Optical Path Length for the axial ray (h=0h=0):

The ray travels through the slab along the principal axis. The refractive index is μ0\mu_0. The OPL for this ray is: OPL0=(refractive index in slab)×(thickness of slab)+(refractive index in air)×(distance in air)OPL_0 = (\text{refractive index in slab}) \times (\text{thickness of slab}) + (\text{refractive index in air}) \times (\text{distance in air}) OPL0=μ0t+1⋅(f−t)OPL_0 = \mu_0 t + 1 \cdot (f-t) OPL0=μ0t+f−tOPL_0 = \mu_0 t + f - t

  1. Optical Path Length for a ray incident at height hh:

A ray incident at height hh enters the slab at (0,h)(0, h). Due to the paraxial approximation (h≪fh \ll f), we assume the ray travels approximately horizontally through the slab at height hh. So, it exits the slab at (t,h)(t, h). The OPL for this part is μ(h)t\mu(h) t. After exiting the slab, the ray travels in air from (t,h)(t, h) to the focal point (f,0)(f, 0). The distance covered in air is (f−t)2+h2\sqrt{(f-t)^2 + h^2}. The refractive index of air is 1. So, the total OPL for this ray is: OPL(h)=μ(h)t+(f−t)2+h2OPL(h) = \mu(h) t + \sqrt{(f-t)^2 + h^2}

  1. Equating the Optical Path Lengths:

For focusing, OPL(h)OPL(h) must be equal to OPL0OPL_0: μ(h)t+(f−t)2+h2=μ0t+f−t\mu(h) t + \sqrt{(f-t)^2 + h^2} = \mu_0 t + f - t

  1. Approximation of the square root term:

Since h≪fh \ll f and t≪ft \ll f, we have h≪(f−t)h \ll (f-t). We can use the binomial approximation A2+B2=A1+(B/A)2≈A(1+12(B/A)2)\sqrt{A^2 + B^2} = A\sqrt{1 + (B/A)^2} \approx A(1 + \frac{1}{2}(B/A)^2) for B≪AB \ll A. Here, A=(f−t)A = (f-t) and B=hB = h. (f−t)2+h2≈(f−t)(1+h22(f−t)2)\sqrt{(f-t)^2 + h^2} \approx (f-t) \left(1 + \frac{h^2}{2(f-t)^2}\right) (f−t)2+h2≈(f−t)+h22(f−t)\sqrt{(f-t)^2 + h^2} \approx (f-t) + \frac{h^2}{2(f-t)}

  1. Substituting the approximation and solving for μ(h)\mu(h):

Substitute the approximated square root term into the OPL equation: μ(h)t+(f−t)+h22(f−t)=μ0t+f−t\mu(h) t + (f-t) + \frac{h^2}{2(f-t)} = \mu_0 t + f - t Cancel (f−t)(f-t) from both sides: μ(h)t+h22(f−t)=μ0t\mu(h) t + \frac{h^2}{2(f-t)} = \mu_0 t Rearrange to solve for μ(h)\mu(h): μ(h)t=μ0t−h22(f−t)\mu(h) t = \mu_0 t - \frac{h^2}{2(f-t)} μ(h)=μ0−h22t(f−t)\mu(h) = \mu_0 - \frac{h^2}{2t(f-t)}

  1. Further approximation (t≪ft \ll f):

Given t≪ft \ll f, we can approximate (f−t)≈f(f-t) \approx f. So, the variation of the refractive index can be represented as: μ(h)≈μ0−h22tf\mu(h) \approx \mu_0 - \frac{h^2}{2tf}

This equation shows that the refractive index decreases quadratically with the distance hh from the principal axis. This is characteristic of a converging gradient-index (GRIN) lens.

The final answer is μ(h)=μ0−h22tf\mu(h) = \mu_0 - \frac{h^2}{2tf}

Explanation of the solution:

For parallel rays to converge at a point, their optical path length (OPL) from the incident plane to the focal point must be constant.

  1. Calculate OPL for the axial ray (h=0h=0): μ0t+(f−t)\mu_0 t + (f-t).

  2. Calculate OPL for a ray at height hh: μ(h)t+(f−t)2+h2\mu(h) t + \sqrt{(f-t)^2 + h^2}.

  3. Equate these OPLs.

  4. Use paraxial approximation (f−t)2+h2≈(f−t)+h22(f−t)\sqrt{(f-t)^2 + h^2} \approx (f-t) + \frac{h^2}{2(f-t)}.

  5. Solve for μ(h)\mu(h): μ(h)=μ0−h22t(f−t)\mu(h) = \mu_0 - \frac{h^2}{2t(f-t)}.

  6. Apply t≪ft \ll f approximation: μ(h)≈μ0−h22tf\mu(h) \approx \mu_0 - \frac{h^2}{2tf}.

Answer:

The variation of refractive index can be represented as: μ(h)=μ0−h22tf\mu(h) = \mu_0 - \frac{h^2}{2tf}