Question

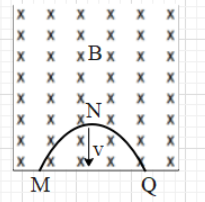
A thin semicircular conducting ring of radius R is falling with its plane vertical in horizontal magnetic induction $\overrightarrow{B}$. At the position MNQ the speed of the ring is V and the potential difference developed across the ring is

A. zero
$\text{B}\text{. }\dfrac{BV\pi {{R}^{2}}}{2}\text{ and M is at higher potential}$
$\text{C}\text{. }\pi RBV\text{ and Q is at higher potential}$
$\text{D}\text{. 2}RBV\text{ and Q is at higher potential}$

Answer 1

The magnitude of the emf or potential difference induced in a conductor is given as $E=\dfrac{d\phi }{dt}$. Magnetic flux is given by $\phi =\overrightarrow{B}.\overrightarrow{A}=BA\cos \theta$. Calculate the change in flux $d\phi$ for a time dt from this instant by calculating the change in area of in time dt. Then $d\phi$ by dt.

Formula used:
$E=\dfrac{d\phi }{dt}$
$\phi =\overrightarrow{B}.\overrightarrow{A}=BA\cos \theta$

Complete answer:
Let us first understand how an emf can be produced in a conductor without connecting the conductor to a cell or a battery. For this, we need to know the Faraday’s law of electro-magnetic induction.
According to the Faraday’s law of electro-magnetic, an emf is produced in conductor when the magnetic flux through the conductor changes with time. This emf is called an induced emf.
This means that if you do not have a cell, then just produce a changing magnetic flux through the conductor (usually a loop). With this, there will be a current in the conductor, if the conductor is closed.
Suppose the magnetic flux through the conductor is $\phi$ then the magnitude of the emf induced in a conductor is given as $E=\dfrac{d\phi }{dt}$.
Magnetic flux is defined as $\phi =\overrightarrow{B}.\overrightarrow{A}=BA\cos \theta$, where $\overrightarrow{B}$ is the magnetic field and $\overrightarrow{A}$ is the area enclosed between the boundary of the conductor. $\theta$ is the angle between them.
In the given case, the ring is just about to come out of the magnetic field. Therefore, the flux will be reduced and thus an emf will be induced inside the ring.
Since the magnetic field is constant
The speed of the ring is given to be v. Hence, from this instant, in the next ‘dt’ time, the ring will be displaced by a distance dx=vdt.
Therefore, the change in area will approximately be dA = 2Rdx = 2Rvdt.
Since the area vector and the magnetic field are parallel, $\theta$=0.
This means that $d\phi =BdA\cos 0=BdA=2RBvdt$.
Hence, $E=\dfrac{d\phi }{dt}=\dfrac{2RBvdt}{dt}=2RBv$.

Hence, the correct option is D.

Note:
Some students may make a mistake by doing the following.
We know that $E=\dfrac{d\phi }{dt}$.
In this case, $E=\dfrac{d\phi }{dt}=B\dfrac{dA}{dt}$.
Area of a semi-circular ring is given as $A=\dfrac{\pi {{R}^{2}}}{2}$.
Therefore, $E=B\dfrac{d\left( \dfrac{\pi {{R}^{2}}}{2} \right)}{dt}=\dfrac{2\pi BR}{2}\dfrac{dr}{dt}$.
This is incorrect because the radius of the ring is not changing with time.