Question

A thin semi-circular conducting ring of radius $R$ is falling with its plane vertical in a horizontal magnetic induction $\overrightarrow{B}$. At the position $MNQ$ the speed of the ring is $v$, and the potential difference developed across the ring is

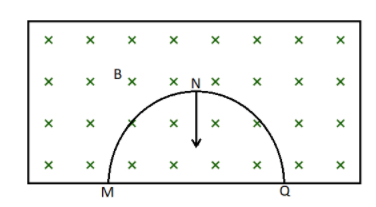
$\begin{aligned} & A.\,\,Zero \\\ & B.\,\,{Bv\pi {{R}^{2}}}/{2}\;\,and\,M\,is\,at\,higher\,potential \\\ & C.\,\,\pi RBv\,and\,Q\,is\,at\,higher\,potential \\\ & D.\,\,2RBv\,and\,Q\,is\,at\,higher\,potential \\\ \end{aligned}$

Answer 1

The potential difference developed across the ring can be found using Faraday’s Law, this will help to get the EMF value. The final position of the semi-circular conducting ring while falling will impact a lot in the calculation of the potential difference.

Formula used:
$ElectroMotive\,Force\,(EMF)=\dfrac{d\phi }{dt}$

Complete step by step answer:
According to the question, A thin semi-circular conducting ring of radius $R$ is falling with its plane vertical in a horizontal magnetic induction $\overrightarrow{B}$, due to which there is magnetic flux that is applied on the circular ring.
So, By Gauss Law, we can say that:
$EMF=\dfrac{d\phi }{dt}$, where $\phi =B.A$
$\Rightarrow EMF=B\dfrac{dA}{dt}$
When the circular ring was about to move out, at that moment:
$dA=2R(vdt)$
$\Rightarrow \dfrac{dA}{dt}=2Rv$
Substituting the value of $\dfrac{dA}{dt}$ in the $EMF$equation, we get:
$EMF=2RBv$
Also, at this moment the point $Q$ will be at higher potential.
Therefore, the correct answer is Option (D).

Additional Information:
Faraday's law of induction (briefly, Faraday's law) is a basic law of electromagnetism predicting how a magnetic field will interact with an electric circuit to produce an electromotive force (EMF)—a phenomenon known as electromagnetic induction. It is the fundamental operating principle of transformers, inductors, and many types of electrical motors, generators and solenoids.

Note:
The final position of the circular ring while falling plays an important role while getting the answer, because at that particular moment the change in area will affect the final answer, so be careful while calculating the potential difference.