Solveeit Logo
Login

Question

Question: A thin semi – circular conducting ring of radius R is falling with its plane vertical in a horizonta...

A thin semi – circular conducting ring of radius R is falling with its plane vertical in a horizontal magnetic induction B⃗\vec B. At the position MNQ the speed of the ring is V, and the potential difference developed across the ring is

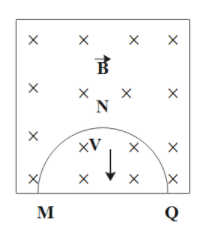
A. Zero
B. BVπR2/2BV\pi {R^2}/2 and M is at higher potential
C. πRBV\pi RBV and Q is at higher potential
D. 2RBV and Q is at higher potential

Explanation

Solution

Faraday's law of induction is a basic law of electromagnetism which is used to predict how a magnetic field would interact with an electric circuit in order to produce an electromotive force, this phenomenon is known as electromagnetic induction. To find the solution of the given question we will use faraday’s law of induction.
Formula Used: ε=−NΔϕΔt\varepsilon = - N\dfrac{{\Delta \phi }}{{\Delta t}}

Complete answer:
The rate of decrease of area of the semi-circular ring is given as,
dAdt=(2R)V\dfrac{{dA}}{{dt}} = \left( {2R} \right)V
The faraday’s second law of electromagnetic induction is defined as the induced emf in a coil which is equal to the rate of change of flux linkage.
Mathematically it is given as,
ε=−NΔϕΔt\varepsilon = - N\dfrac{{\Delta \phi }}{{\Delta t}}
Where ‘ε\varepsilon ’ is expressed as the electromotive force, ‘ϕ\phi ’ is expressed as the magnetic flux, and ‘N’ is expressed as the number of turns.
The negative (-) sign in the formula indicates the direction of the induced emf and change in the direction of magnetic fields have opposite signs.
Now, according to the faraday’s second law of induction of induced emf,
e=−dϕdt=−BdAdt=−B(2RV)e = - \dfrac{{d\phi }}{{dt}} = - B\dfrac{{dA}}{{dt}} = - B\left( {2RV} \right)
∴e=2BRV\therefore e = 2BRV
The induced current in the ring must generate a magnetic field in the upward direction. So, Q is at a higher potential.
Thus, the potential difference developed across the ring is 2RBV and Q is at higher potential.

Hence, option (D) is the correct answer.

Note:
We see that the Lenz law is reflected in the faraday’s law. Lenz law is defined as the induced electromotive force with non – identical polarities which induces a current whose magnetic field opposes the change in the magnetic flux through the loop in order to make sure that the original flux is maintained through the loop when current flows in it.