Question
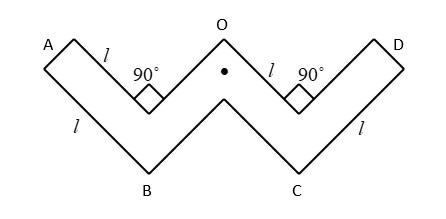
Question: A thin rod of length 4l, mass 4m is bent at the points as shown in the figure. What is the moment of...
A thin rod of length 4l, mass 4m is bent at the points as shown in the figure. What is the moment of inertia of the rod about the axis passing point O and perpendicular to the plane of the paper?
A) 3ml2
B) 310ml2
C) 12ml2
D) 24ml2
Solution
Recall the concept of moment of inertia. We must also know how to calculate the moment of inertia for the rod about different axis. We need to know about the parallel axis theorem to be able to solve this problem.
Complete step by step solution:
The force needed for a required acceleration is determined by the mass. In a similar way, the torque needed for a required angular acceleration is determined by the moment of inertia.
I=ωL
Where I is the moment of inertia
L is the angular momentum
ω is the angular velocity
Mathematically, moment of inertia is expressed as the summation of the product of mass of each particle and the square of the distance of the particle from the axis of rotation.
⇒I=∑miri2
SI unit of moment of inertia is kg⋅m2 .Its dimensional formula is given by [ML2] .
The moment of inertia of rod can be given at the central axis. For any other axis other than the central axis, the moment of inertia can be calculated by the parallel axis theorem.
If an axis of rotation of the body is parallel to the central axis, then the parallel axis theorem states that the moment of inertia of the body about that axis is equal to the sum of the moment of inertia about the central axis and the product of the mass of the body and square of the distance between the two axis.
⇒I=Ic+Mh2
Where I is the moment of inertia about the axis parallel to the central axis
Ic is the moment of inertia about the central axis
M is mass of the body
h is the distance between the central and the parallel axis
So, now we calculate the moment of inertia of rod of length l about the end axis
⇒Iend=Ic+Mh2
The distance between the end and the centre is 2l
⇒Iend=12ml2+4ml2
(∵ moment of inertia about central axis is 12ml2 )
⇒Iend=3ml2
⇒ The moment of inertia of AB about the axis B is I1=3ml2 .
⇒ The moment of inertia of CD about the axis C is I2=‘3ml2 .
⇒ The moment of inertia of BO about the axis O is I3=3ml2 .
⇒ The moment of inertia of OC about the axis O is I4=3ml2 .
Now, again we use the parallel axis theorem to calculate the moment of inertia of AB and CD about the axis O .
Moment of inertia of AB about O is I5=3ml2+ml2
⇒I5=34ml2
Similarly, moment of inertia of CD about the axis O is I6=34ml2
Now that we know all the moments of inertia acting about the axis O , we add them to get the total moment of inertia about O .
⇒I=I3+I4+I5+I6
⇒I=3ml2+3ml2+34ml2+34ml2
⇒I=310ml2
Therefore, option (B), I=310ml2 is the correct option.
Note: The moment of inertia of an object is also known as the mass moment of inertia of the object. There are two axis theorems namely the parallel axis theorem and the perpendicular axis theorem. Do not confuse between the parallel and perpendicular axis theorem.
