Question
Question: A thin rod of length \(4l\) , mass \(4m\) is bent at the points as shown in figure. What is the mome...
A thin rod of length 4l , mass 4m is bent at the points as shown in figure. What is the moment of inertia of the road about the axis passing point O and perpendicular to the plane of the paper.
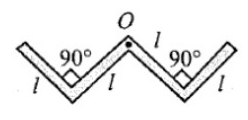
A.3Ml2
B.310Ml2
C.12Ml2
D.24Ml2
Solution
Relation between the moment of inertia and mass
I=mr2
Where m= is the mass
And I= moment of inertia
Complete step by step answer:
First, we know about the moment of inertia
Moment of inertia:- Moment of inertia is defined as the product of the mass of section and the square of the distance between the reference axis and the centroid of the section.
It is defined as I.
I=mr2
Or
Moment of inertia I is defined as the ratio of the net angular momentum of a system to its angular velocity around a principal axis. That is
I=ωL
Where I= Moment of inertia
L= Angular momentum of a system
ω= Angular velocity
Since the length of the rod is 4l and mass 4m
Length of AB=BO=OC=CD=l
Mass=m (for all length part)
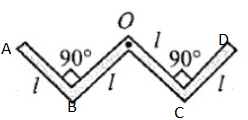
Moment of inertia of a rod about to end =3ml2
Moment of inertia of AB, BO, OC, CD about B, D, C respectively =3ml2
From parallel axis theorem,
Moment of inertia of AB about O
=3ml2+ml2
=34ml2
Similarly on CD about O,
=34ml2
So moment of inertia of rod about O
I=3ml2+3ml2+34ml2+34ml2
I=310ml2
Note:
Student takes the same formula for both sidewise rotation and around the centre but the formula for both are different.
