Question

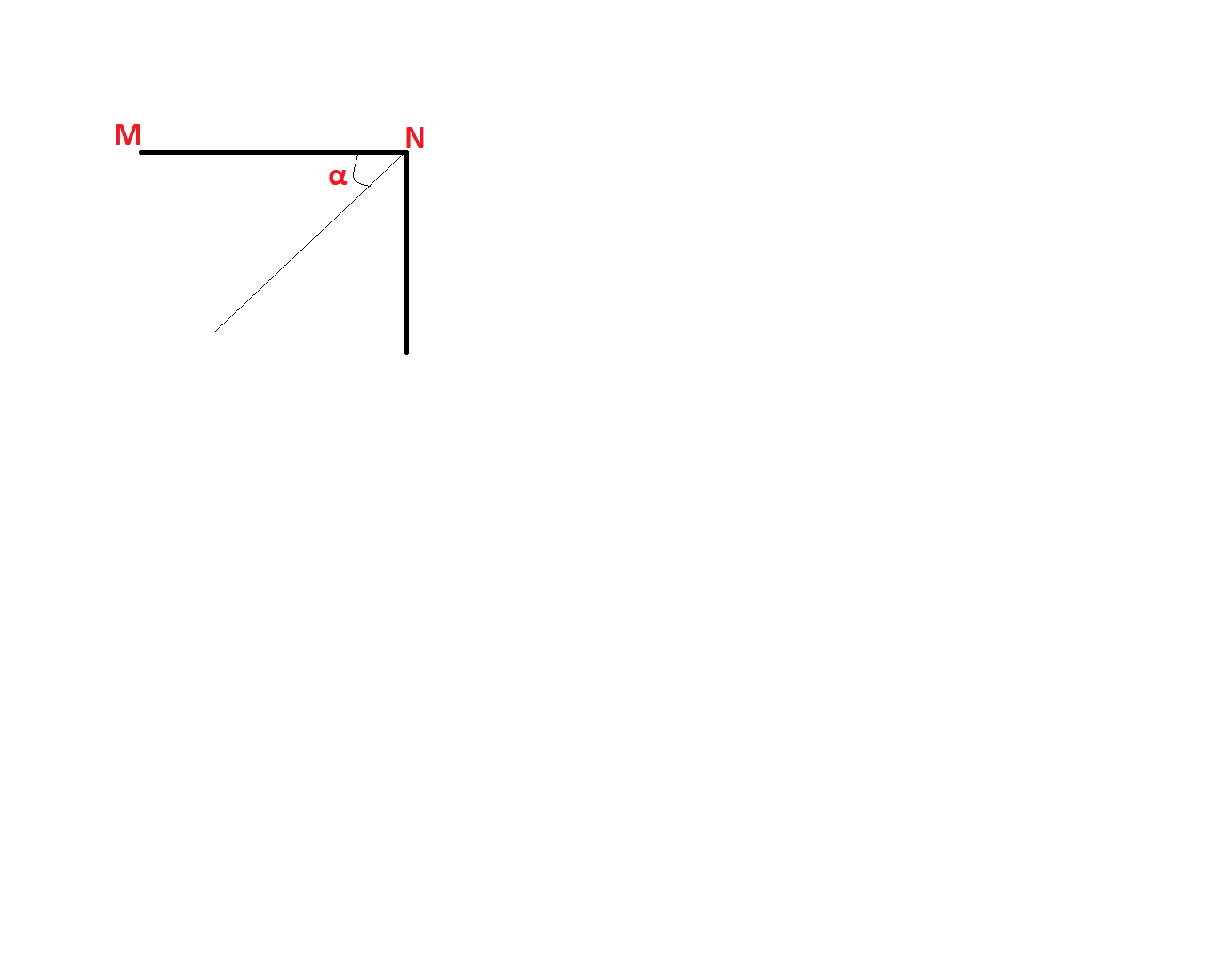
A thin rod MN, free to rotate in the vertical plane about the fixed end N, is held horizontal. When the end M is released the speed of this end, when the rod makes an angle a with the horizontal, will be proportional to: (see figure)

A. $\sqrt {\cos \alpha }$
B. $\cos \alpha$
C. $\sin \alpha$
D. $\sqrt {\sin \alpha }$

Answer 1

Using the law of conservation of energy, we will find out the relationship between potential and kinetic energy of the rod in its original and rotated state. From there we get the value of its angular velocity upon rotation. This angular velocity value will be used to determine the velocity of the free end.

Formula used:
Kinetic energy of the rod: ${E_k} = \dfrac{1}{2}I{\omega ^2}$
Where $I$ is the moment of inertia of the rod and is expressed in meter to the power four $({m^4})$, $\omega$ is the angular velocity and is expressed radians per second $(rad - {s^{ - 1}})$ and ${E_k}$ is the kinetic energy of the rod upon rotation and is expressed in Joules $(J)$.
Potential energy of the rod: ${E_P} = Mgl \times \sin \theta$
Where $l$ is the length of the rod and is expressed in meter $(m)$, $M$ is the mass of the rod and is expressed in kilograms $(kg)$, and $g$ is the acceleration due to gravity and is approximated as $9.8m/{s^2}$, $\theta$ is the angle of rotation and is expressed in radians $(rad)$ and ${E_P}$ is the potential energy of the rod in horizontal position and is expressed in Joules $(J)$.

Complete step by step answer:
When the free end of the rod $M$ is rotated about its fixed position $N$ in the vertical plane, it rotates with angle of $\alpha$. This is given.
Let us assume the following data:
Length of rod:
Mass of rod:
Velocity of rod:
Rod is homogenous, which means its center of gravity lies at its mid-section.
Let's assume two positions of the given rod:
$I$ at horizontal, initial position
$II$ at an angle of $\alpha$, rotated

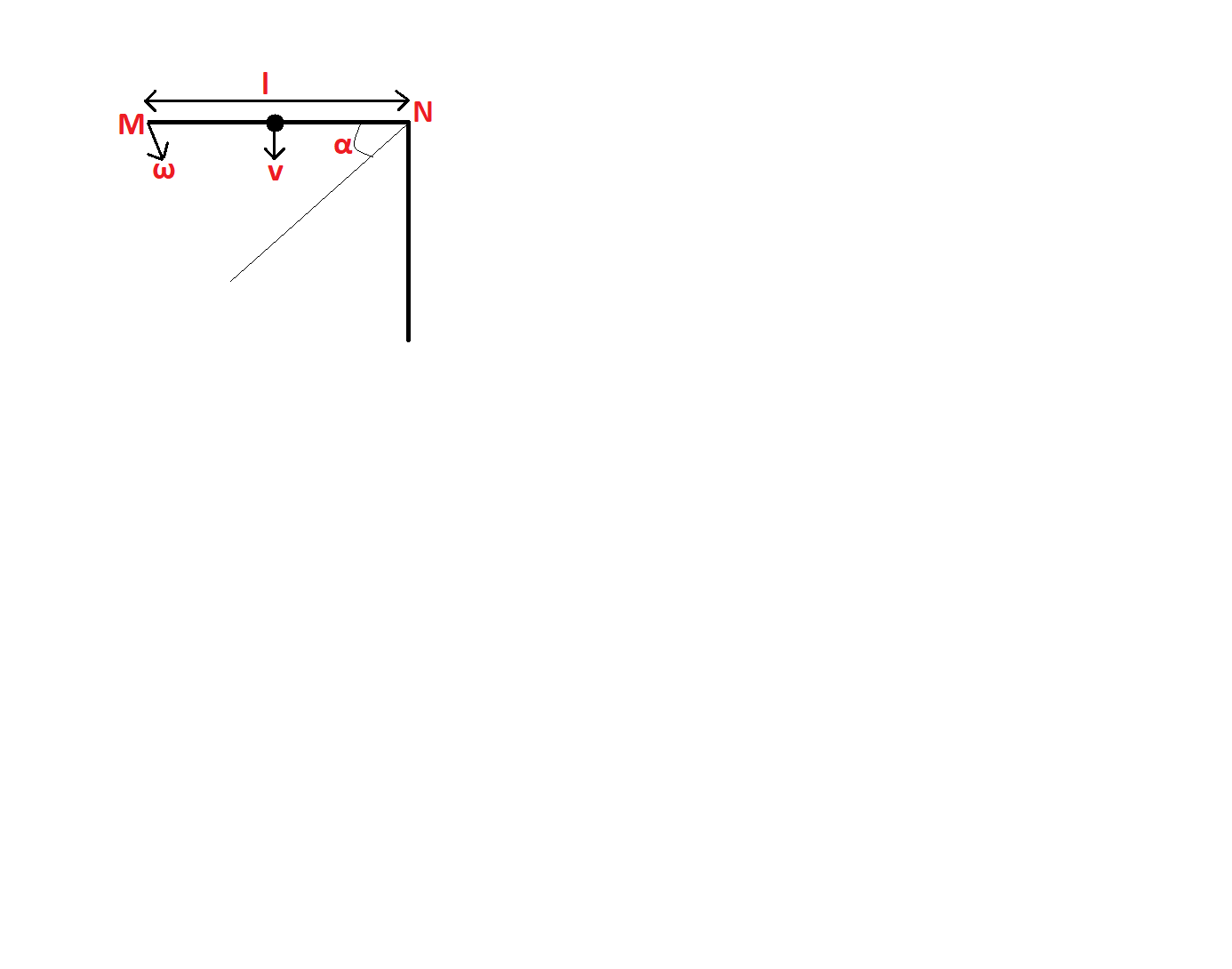
We know that the potential energy stored in the rod at horizontal position will be converted to kinetic energy. It also means that they both will be equal in magnitude, according to the law of conservation of energy.
Now, at state $II$ we have kinetic energy due to rotation about $N$ to be
${E_k} = \dfrac{1}{2}I{\omega ^2}$
And at state $I$ we have the potential energy to be
${E_P} = Mgl \times \sin \theta$
As assumed above, the rod is homogenous. Therefore, its mass acts at the center of gravity. Therefore, $l = \dfrac{l}{2}$ for our rod.
When we substitute the values of length, mass and angle of rotation in the potential energy formula we get,
${E_P} = Mgl \times \sin \theta = Mg\dfrac{l}{2}\sin \alpha \\\ \Rightarrow {E_P} = Mg\dfrac{l}{2}\sin \alpha \\\$
But this is equal to kinetic energy.

Therefore,
${E_P} = {E_K} \\\ \Rightarrow Mg\dfrac{l}{2}\sin \alpha = \dfrac{1}{2}I{\omega ^2} \\\$
We know that, for a rod, $I = \dfrac{{M{L^2}}}{3}$.
Upon substitution we get,
$Mg\dfrac{l}{2}\sin \alpha = \dfrac{1}{2}I{\omega ^2} = \dfrac{1}{2}(\dfrac{{M{L^2}}}{3}){\omega ^2} \\\ \Rightarrow \omega = \sqrt {\dfrac{{3g}}{l}\sin \alpha } \\\$
But, $v = \omega l$
Therefore,
$v = \omega l = \sqrt {\dfrac{{3g}}{l}\sin \alpha } \times l$
Taking $l$ under the root we get,
$v = \sqrt {\dfrac{{3g}}{l} \times {l^2}} \times \sqrt {\sin \alpha }$
We know that $g,l$ are constants for the given rod.
Therefore we deduce that $v \propto \sqrt {\sin \alpha }$

So, the correct answer is “Option D”.

Note:
The approximation that the rod is homogenous simplified our calculations.
As nothing is mentioned, we assumed this. In case the distribution of mass of the rod is mentioned, the value of length would have been different.