Question

A thin prism having refracting angle ${10^ \circ }$ is made of glass of refractive index $1.42$. This prism is combined with another thin prism of glass of refractive index $1.7$. This combination produces dispersion without deviation. The refracting angle of the second prism should be:
(A) ${10^ \circ }$
(B) ${4^ \circ }$
(C) ${6^ \circ }$
(D) ${8^ \circ }$

Answer 1

Use the relation given below and substitute the values of the refractive angle of the first prism and the refractive index of the two prisms in it. The output provides the refractive angle of the second prisms. This both the prisms make the light wave disperse in it.

Useful formula:
The refractive relation in the prism is given by
${\theta _1}\left( {{r_1} - 1} \right) = {\theta _2}\left( {{r_2} - 1} \right)$
Where ${\theta _1}$ is the refractive angle of the first prism, ${\theta _2}$ is the refractive angle of the prism two, ${r_1}$ is the refractive index of the glass of the first prism and ${r_2}$ is the refractive index of the glass of the second prism.

Complete step by step solution:
It is given that the
Refractive angle of the first prism, ${\theta _1} = {10^ \circ }$
The refractive index of the glass in the first prism, ${r_1} = 1.42$

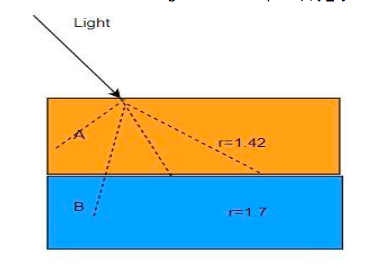
The refractive index of the glass in the first prism, ${r_1} = 1.7$
Using the formula of the relation,
${\theta _1}\left( {{r_1} - 1} \right) = {\theta _2}\left( {{r_2} - 1} \right)$
Substituting the known values in the above relation,
$10\left( {1.42 - 1} \right) = {\theta _2}\left( {1.7 - 1} \right)$
By performing the simplification inside the brackets
$10\left( {0.42} \right) = {\theta _2}\left( {0.7} \right)$
By grouping the similar terms on one side and the unknown parameter on the other side.
$\dfrac{{10 \times 0.42}}{{0.7}} = {\theta _2}$
By performing the simple arithmetic operations,
${\theta _2} = {6^ \circ }$
Hence the refractive index of the second prism is obtained as ${6^ \circ }$.

Thus the option (C) is correct.

Note: The disperse index of the water is $1$. Thus the relation contains this term. It is defined as the layer of the object that slowdowns the speed of the light through it and maintains its dispersion there. In this condition, the two prisms are connected together with a high refractive index making light to disperse inside.