Question
Question: A thin plate AB of large area A is placed symmetrically in a small gap of height h filled with water...
A thin plate AB of large area A is placed symmetrically in a small gap of height h filled with water of viscosity η0 and the plate has a constant velocity v by applying a force F as shown in the figure. If the gap is filled with some other liquid of viscosity0.75η0 , at what minimum distance (in cm) from top wall should the plate be placed in the gap, so that the plate can again be pulled at the same constant velocity v, by applying the same force F? (Take h=20cm).
Solution
Since a viscous liquid is filled in the gap, the force experienced by the plate is the viscous force. Now recall the expression for viscous force and then find the viscous force exerted by the liquid column above and below the plate acting on the plate when the plate is kept symmetrically in the gap, that is, equidistant from both walls. Now equate this force to the force on the plate when the liquid is replaced by another liquid of different viscosity such that velocity remains the same and then find the minimum distance from the top wall.
Formula used: Expression for the viscous force,
F=lηAv
Complete step by step answer:
In the question we are given a thin plate AB which is kept in a small gap or channel with a height h and is also filled with a liquid of viscosityη0. On applying a force F the plate acquires a velocity v. Now we are filling the gap with another liquid with viscosity 0.75η0 and we are asked to find the minimum distance at which the plate should be kept from the top wall such that the plate will have the same velocity v on applying the same force F.
Let us revise what is a viscous force. When there is a relative motion between the layers of the liquid the viscous force comes into picture providing a resistance to fluid motion. Unlike in the case of solids, stress here depends on the strain rate or the rate of change of strain (lΔtΔx) or(lv). So the coefficient of viscosity is given by,
η=(lv)(AF)
η=vAFl
Where F is the viscous force, l is the length of the liquid column, A is the area of the small gap, v is the velocity of the liquid.
F=lηAv ………………………………….. (1)
Now let us apply this for the first case where the plate is kept symmetrically, that is, l=2h
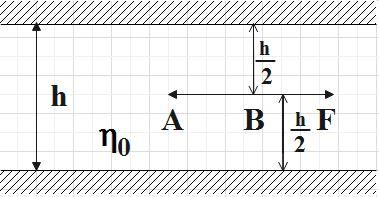
Liquid column above the plate as well as below the plate exerts viscous force on it.
So for the first case (1) becomes,
F=F1+F2=2hη0Av+2hη0Av
F=4hη0Av ………………………… (2)
Now for the second case, let the plate be kept at y distance from the top wall, then,
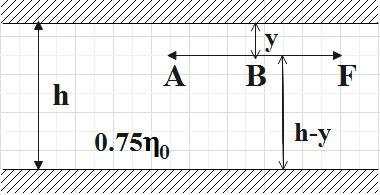
F=F1+F2=y0.75η0Av+h−y0.75η0Av
⇒F=0.75η0Av(y1+h−y1)=0.75η0Avyh−y2h ……………………… (3)
Since the force exerted is the same here, we could equate (2) and (3),
4hη0Av=0.75η0Avyh−y2h
⇒yh−y2=40.75h2
But h=20cm in the question,
⇒20y−y2=4400×0.75=75
⇒y2−20y+75=0
⇒(y−15)(y−5)=0
⇒y=5cm / y=15cm
Since we are asked to find the minimum distance at which the plate is kept from the top wall, y=5cm is the required answer.
Hence, the minimum distance (in cm) from the top wall at which the plate should be placed in the gap, so that the plate can be pulled at the same constant velocity v, by applying the same force F is 5cm.
Note: While solving we are getting a quadratic equation in y and we know that a quadratic equation has two roots. But you are supposed to go for the least possible value since we are asked the minimum distance. Also in this type of questions figures do a very important role in guiding you to the solution, so make a rough sketch while you read the question.
