Question
Question: A thin metallic spherical shell of radius R carries a charge Q on its surface. A point charge \(\dfr...
A thin metallic spherical shell of radius R carries a charge Q on its surface. A point charge 2Q is placed at its center C and another charge +2Q is placed outside the shell at a distance x from the centre as shown in the figure. Find (i) force on the charge at the centre of the shell and at point A. (ii)the electric flux through the shell.
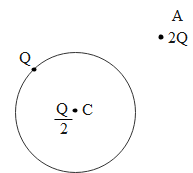
Solution
The determine the electrostatic force at any point in the above system we need to obtain the electric field at that point. Hence further using the relation between the electric field and force on a charge, we can determine the magnitude of the force acting on the charge at the required point. To determine the flux we can use Gaussian expression can be used for flux across a closed surface.
Formula used:
ϕ=∈∘q
ϕ=EΔS
F=EQ
Complete answer:
Let us say there is a charge ‘q’ enclosed by a closed surface. If ∈∘ is the permittivity of free space, the flux ϕ through the closed surface is given by,
ϕ=∈∘q.....(1)
If the electric field at the surface closed surface is ‘E’ and the surface area of the closed Gaussian surface is ΔS, the total flux across the closed is also given by,
ϕ=EΔS.....(2)
Let us enclose the spherical shell in a closed spherical Gaussian surface of radius ‘x’. Hence the flux through the closed surface from equation 2 is given by,
ϕ=EΔS∴ϕ=E4πx2.....(3)
The total charge ‘q’ enclosed by the Gaussian surface is,
q=Q+2Q=23Q
Hence using equation 1, the flux through the spherical surface of radius ‘x’ is given by,
ϕ=∈∘q∵q=23Q∴ϕ=∈∘23Q=2∈∘3Q.....(4)
Equating equation 3 and 4 we obtain,
E4πx2=2∈∘3Q⇒E=23(4π∈∘x2Q)
The electric force (F) experienced by the charge Q=+2Q is placed outside the shell at a distance x is given by,
F=EQ∵E=23(4π∈∘x2Q), Q=+2Q⇒F=23(4π∈∘x2Q)(+2Q)∴F=(4π∈∘x23Q2)
Therefore the force on charge +2Q is equal to 4π∈∘x23Q2.
The electric field inside a closed metallic surface is zero. Hence the force experienced by the charge placed at the centre C is also zero.
The flux through the metallic spherical shell is equal to,
ϕ=∈∘q∵q=23Q⇒ϕ=∈∘23Q=2∈∘3Q
Note:
The above expression for flux can only be obtained for closed Gaussian surface. The flux through the surface does not depend on the radius of the surface. It only depends on the medium enclosed within the surface and the charge enclosed.
