Question

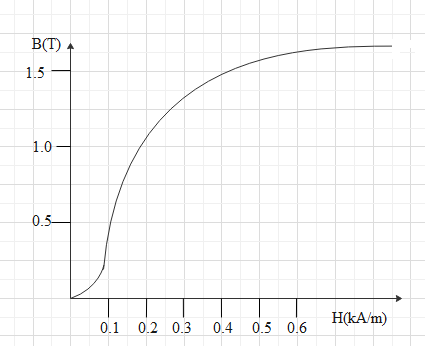
A thin iron ring with mean diameter $d=50cm$ supports winding consisting of $N=800$ turns carrying current $I=3.0A$. The ring has a cross-cut of width $b=2mm$. Neglecting the scattering of the magnetic flux at the gap edges, and using the plot shown in the figure below, find the permeability of iron under these conditions.

Answer 1

First we will draw the diagram for the ring, then by applying Ampere circuital law, we can find an equation for straight line relating magnetic field, B and magnetic field strength. Once we get the equation of the straight line we can plot it in the given graph and then find the intersection of the given curve and the straight line which will give the value of B and H. Finally we can find the value of permeability of iron using the value of B and H.

Formula used:

& \oint{H.dl=NI} \\\ & H=\dfrac{B}{\mu } \\\ \end{aligned}$$ **Complete step by step answer:** The thin iron ring which is given here can be shown as follows 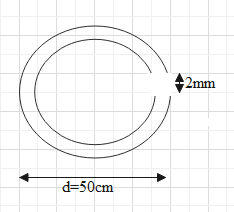 On the given ring there is winding having 800 turns and current of 3A. Now the magnetic field strength can be given by Ampere circuital law which states that the line integral of the magnetic field strength for a material is equal to the current flowing through it. $$\oint{H.dl=NI}$$ Here H is magnetic field strength and dl is the infinitesimal length and N is the number of turns and I is the current. Now if we apply the line integral on the ring we get $$H(d\pi -b)+H'(b)=NI\text{ }...............\text{(i)}$$ H is the field strength of the ring excluding the cross cut part (therefore b is subtracted from dπ) and H’ is field strength from the cross cut part. Now the cross cut part is in vacuum therefore H’ can be given as $$H'=\dfrac{B}{{{\mu }_{0}}}$$ Where $${{\mu }_{0}}$$is the permeability in free space. Substituting this in equation (i), we get $$\begin{aligned} & H(d\pi -b)+\dfrac{B}{{{\mu }_{0}}}(b)=NI \\\ & \Rightarrow \dfrac{B}{{{\mu }_{0}}}b=NI-H(d\pi -b) \\\ & \Rightarrow B=\dfrac{{{\mu }_{0}}}{b}\left[ NI-H(d\pi -b) \right] \\\ \end{aligned}$$ Now we have given the values of d, b, N and I which are $$d=50cm=0.5cm,b=2mm=0.002m,N=800\text{ and }I=3.0A$$. We know π and $${{\mu }_{0}}$$are constants having values $$\pi =3.14\text{ and }{{\mu }_{0}}=1.26\times {{10}^{-6}}N{{A}^{-2}}$$ Substituting all these values in above equation we get $$\begin{aligned} & B=\dfrac{1.26\times {{10}^{-6}}}{0.002}\left[ \left( 800 \right)\left( 3 \right)-H(0.5\left( 3.14 \right)-0.002) \right] \\\ & \Rightarrow B=6.3\times {{10}^{-4}}\left[ 2400-H(1.57-0.002) \right] \\\ & \Rightarrow B=6.3\times {{10}^{-4}}\left( 2400-1.568H \right) \\\ & \Rightarrow B=1.512-(0.987\times {{10}^{-3}})H\text{ }......................\text{(ii)} \\\ \end{aligned}$$ Now we can see from the graph that value of H is in kA/m instead of A/m, therefore we can write equation (ii) as $$B=1.512-0.987H\text{ }...............\text{(iii)}$$ Now equation (iii) represents equation of straight line, let us find some points for B respected to H H| $$B=1.512-0.987H$$ ---|--- $$H=0.1$$| $$B=1.4113$$ $$H=0.2$$| $$B=1.3146$$ $$H=0.3$$| $$B=1.2159$$ Plotting these points in the given graph we get 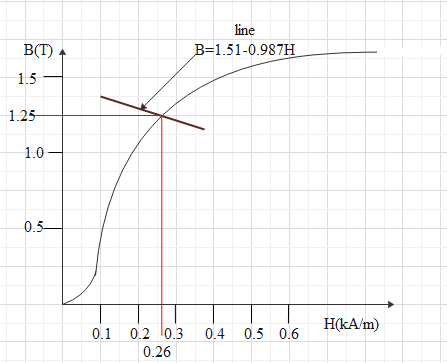 The straight line for equation (iii) is shown by the brown line and values of B and H which we get at the intersection of the curve given and the straight line is shown by red lines. So the values of B and H we get from the above graph are $$B=1.25T\text{ and }H=0.26kA{{m}^{-1}}$$. Now the relation between H and B is given by the formula $$H=\dfrac{B}{\mu }$$ Where μ is the permeability of the material. Hence by using this formula we can find the permeability of iron rings. So rewriting above formula for permeability we get $$\mu =\dfrac{B}{H}$$ Now substituting the value of H and B we obtained from graph, we get $$\begin{aligned} & \mu =\dfrac{1.25T}{0.26\times {{10}^{3}}A{{m}^{-1}}} \\\ & \mu =4.0807\times {{10}^{-3}}N{{A}^{-2}} \\\ \end{aligned}$$ **Hence permeability of iron under these conditions will be $$4.0807\times {{10}^{-3}}N{{A}^{-2}}$$.** **Note:** Mostly permeability is measured in henry per meter i.e. H/m but to avoid confusion between magnetic field strength and henry we used another unit of permeability. Also note here we calculated permeability of a material and not the relative permeability which can be given by the ratio of permeability of a material to the permeability in free space.