Question
Question: A thin horizontal disc of radius \(R = 10\;cm\) is located within a cylindrical cavity filled with o...
A thin horizontal disc of radius R=10cm is located within a cylindrical cavity filled with oil whose viscosity η=0.08P(figure shown above). The clearance between the disc and the horizontal planes of the cavity is equal toh=1.0mm. Find the power developed by the viscous forces acting on the disc when it rotates with the angular velocity ω=60rad/s. The end effects are to be neglected. Round off to the closest integer.
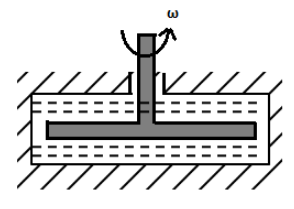
Solution
As the disc is rotating, four of viscosity arises due to velocity gradient. A torque is developed on the both upper and the lower clearance ends and thus power is developed. The power is the product of torque and angular velocity.
Formula used:
1. Four of viscosity, F=ηAdxdv
2. Torque, τ=rF
3. Power, P=τ×ω
Where η is the coefficient of velocity, A is the area of surfaces in contact, dxdv is the velocity gradient, r is the radius and ω is the angular velocity.
Complete step by step answer:
When the disc rotates the fluid in contact also rotates in the same manner as the disc. However, the fluid with the walls of the cavity does not rotate. So, there is a difference in velocity with distance. This leads to a set up of velocity gradient due to viscous forces. Now, the linear velocity at distance r from axis, v=rω. As it varies with h, so, velocity gradient,
dxdv=hωr …. (1)
Where, ω denotes the angular velocity.
So, the viscosity force by Newton’s law is given by
F=ηAdxdv
Now, area, A=2πrdr
So, from equation (1), we can write, df=η2πrdr×hωr
df=n2πr2dr×hω
So, the torque due to this force is
dτ=rdF ⇒dτ=r×η2πr2drhω
⇒dτ=η2πr3drhω
Net torque due to upper and lower clearance is,
Now, power developed, P=τω
P=ηhπR4ω2
As R = radius of disc = 10cm=0.1m
η=0.08p ⇒h=1.0mm=1×10−3m ⇒ω=60rad/sec
So, P=10−30.08×3.14×(0.1)4×(60)2
∴P=9.05watt
Hence, the power developed by viscous force is 9.05watt.
Note: As the disc has Radius R. So, considering the centre of disc as origin, the value of ends is from –R to R, So, dr varies from –R to R. In linear motion, the power is the product of the force and velocity but in the rotational motion, the force is replaced by the torque and the velocity is replaced by the angular velocity. Note that the units of all the quantities must be in the S.I units.
