Question

A thin hoop of weight $500N$ and radius $1m$ rests on a rough inclined plane as shown in the figure. What is the minimum coefficient required for this setup:

A. $\dfrac{1}{{3\sqrt 3 }}$
B. $\dfrac{1}{{\sqrt 3 }}$
C. $\dfrac{1}{2}$
D. $\dfrac{1}{{2\sqrt 3 }}$

Answer 1

Hint Find the maximum friction force. As the hoop is in rest –
$T \times R = {F_f} \times R$
So, the force by upper rope becomes $\dfrac{{mg\sin \theta }}{2}$
The summation of friction force and force by upper rope is $mg\sin \theta$.
So, for the coefficient to be minimum, the friction force is equal to the maximum friction force.

Complete step-by-step solution :Let the force by upper rope be $T$ and the friction force acting on the hoop be ${F_f}$.
Let the coefficient of friction be $\mu .$

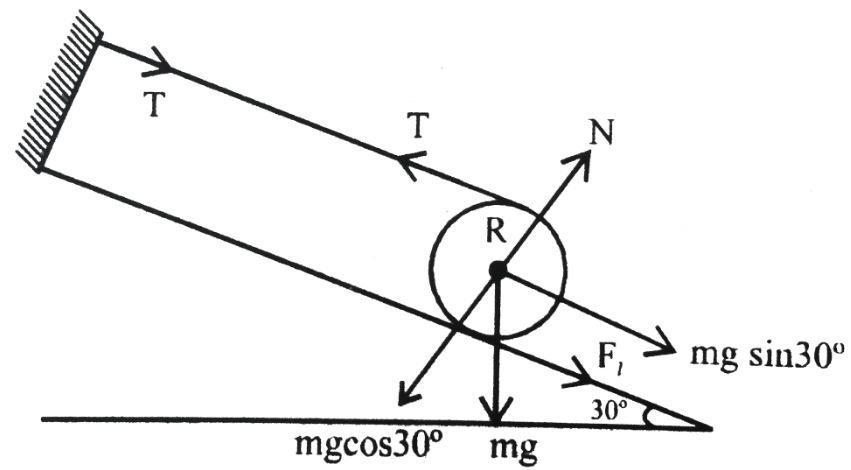
The Normal force acting perpendicular to the plane –
$N = mg\cos {30^ \circ }$
where, $m$ is the mass and $g$ is the acceleration due to gravity which is equal to $10m{s^{ - 2}}$.
Therefore, the maximum friction force acting on hoop is –
${F_f} = \mu N \\\ {F_f} = \mu mg\cos {30^ \circ } \cdots (1) \\\$
Now, as the hoop is in rest, therefore, for the rotational equilibrium about centre of mass –
$T \times R = {F_f} \times R \\\ \therefore T = {F_f} \cdots (2) \\\$
Now, force balance along the incline so, the translation equilibrium along the plane –
$T + {F_f} = mg\sin {30^ \circ } \cdots (3)$
Therefore, from equation $(2)$ and $(3)$, we get –
${F_f} + {F_f} = mg\sin {30^ \circ } \\\ 2{F_f} = mg\sin {30^ \circ } \\\ {F_f} = \dfrac{{mg\sin {{30}^ \circ }}}{2} \cdots (4) \\\$
To find out the minimum value of coefficient of the configuration we have to take equation $(1)$ and equation $(4)$ -
Therefore, from equation $(1)$ and equation $(4)$ , we get –
$\dfrac{{mg\sin {{30}^ \circ }}}{2} = \mu mg\cos {30^ \circ }$
Cancelling $mg$ on both sides and doing cross – multiplication, we get –
$\mu = \dfrac{{\tan {{30}^ \circ }}}{2} \cdots (5)$
We know that,
$\tan {30^ \circ } = \dfrac{1}{{\sqrt 3 }}$
Putting the value of $\tan {30^ \circ }$ in equation $(5)$, we get –
$\mu = \dfrac{1}{{2\sqrt 3 }}$
So, the minimum required coefficient of friction is $\dfrac{1}{{2\sqrt 3 }}$.
Hence, option (D) is the correct option.

Note:- Centre of mass of a body is the point where all of the mass of the body is situated and the object is said to be in equilibrium if all the forces acting on the object in the same plane are balanced and there is no net force. So, when the hoop was in the rest the equilibrium at centre of mass was –
$T \times R = {F_f} \times R$