Question

A thin half ring of radius $R = 20cm$ is uniformly charged with a total charge $q = 0.70nC$. The magnitude of electric field strength at the curvature centre of this half ring is:
A. $100V/m$
B. $20V/m$
C. $225V/m$
D. $4V/m$

Answer 1

In this problem, to find the magnitude of electric field strength at the curvature centre of the half ring, we will consider this ring consists of a large number of very small arcs. Then we will consider one such small segment and then integrate its horizontal and vertical components of electric field strength to determine the required magnitude of electric field strength at the curvature centre.

Formula used:
$E = \dfrac{{kq}}{{{R^2}}}$,
where $E$ is the electric field strength, $k$ is the constant with a value $8.99 \times {10^9}N{m^2}/s$, $q$ is the total charge and distance of the point from the charged surface.

Complete step by step answer:
Let us first consider a very small arc element. Let it be lying at an angle $\theta$ with respect to the x-axis and subtending a small angle $d\theta$at the centre of the curvature of the half ring as shown in figure.

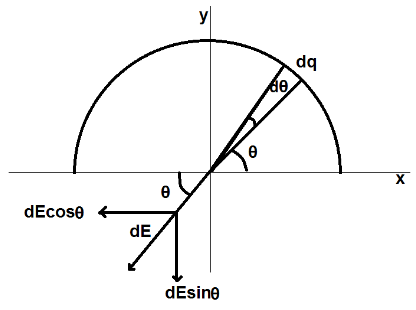
Let the charge on the small element be $dq = \dfrac{q}{\pi }d\theta$ which can be assumed to be a point charge. Now, the small electric field produced by this small arc element carrying $dq$ charge is given by
$dE = \dfrac{{k\left( {dq} \right)}}{{{R^2}}}\\\ \Rightarrow dE = \dfrac{k}{{{R^2}}}\left( {\dfrac{q}{\pi }d\theta } \right) \\\ \Rightarrow dE = \dfrac{{kqd\theta }}{{\pi {R^2}}}$
Now, we will find the horizontal and vertical component of the total electric field strength by integrating this small electric field.
First, the horizontal component is given by
${E_x} = \int\limits_{\theta = 0}^{\theta = \pi } {dE\cos \theta } \\\ \Rightarrow {E_x} = \int\limits_0^\pi {\dfrac{{kq}}{{\pi {R^2}}}} \cos \theta d\theta \\\ \Rightarrow {E_x} = 0$

As the horizontal component is zero, the total electric field is same as its vertical component which is given by
$E = {E_y} \\\ \Rightarrow E = \int\limits_{\theta = 0}^{\theta = \pi } {dE\sin \theta } \\\ \Rightarrow E = \int\limits_0^\pi {\dfrac{{kq}}{{\pi {R^2}}}} \sin \theta d\theta$

\Rightarrow {E_y} = \dfrac{{2kq}}{{\pi {R^2}}}$$ Thus, the total electric field strength at the curvature centre of this half ring is given by $E = \dfrac{{2kq}}{{\pi {R^2}}}$ Putting the given values $$R = 20cm$$, $$q = 0.70nC$$and $k = 8.99 \times {10^9}N{m^2}/s$ $$\therefore E = \dfrac{{2 \times 8.99 \times {{10}^9} \times 0.70 \times {{10}^{ - 9}}}}{{\pi \times {{0.2}^2}}} \approx 100V/m$$ **Hence, option A is the right answer.** **Note:** Here, we have seen from the integration of horizontal components that total electric field strength has zero value of its horizontal component. It can also be seen directly without doing integration from the symmetry that the direction of resultant electric field would be along the line of symmetry which is y-axis. Therefore, we can integrate directly for vertical components of electric field strength.